
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) ( 23 ) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (111) (112) (113) (114) (115) (116) (117) (118) (119) (120) (121) (122) (123) (124) (125) (126) (127) (128) (129) (130) (131) (132) (133) (134) (135) (136) (137) (138) (139) (140) (141) (142) (143) (23) жет иметь любые значения в некоторых пределах ном±А. При стрельбе по цели снаряд может оказаться как ближе, так и дальше цели и расстояние от орудия до места попадания снаряда может быть любым в некоторых пределах. Случайная величина называется непрерывной, если ее возможные значения занимают сплошь некоторый интервал. Плотность распределения. Вероятность попадания случайной величины в одинаковые интервалы ее значений различна. Например, если изготавливается конденсатор с номинальным значением емкости 1 ООО пф, то в интервале 900-1 ООО пф окажется большее их количество, чем в интервале 800-900 пф. Отношение вероятности попадания величины х в интервал Ах к величине этого интервала называется плотностью распределения вероятности: 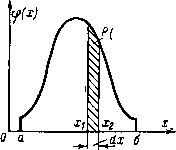 Рис. 4-3. Плотность распределения Случайной величины. 9{х) Р{Хг<Х<{Хг-\-1х)} Зная плотность распределения, можно определить вероятность P{xi<x<{xi+Ax)}=<p{x)Ax. Плотность распределения, заданная для всех возможных значений х, полностью характеризует случайную величину и представляет собой закон ее распределения. Графическое изображение закона распределения непрерывной случайной величины называется кривой распределения вероятностей (рис. 4-3)-Если все возможные значения х находятся в пределах аб, то попадание зна- чения X в интервал аб является достоверным событием. Поэтому Вероятность попадания значения случайной величины в произвольный интервал хх определяется из равенства P{x,<x<x,)=-<9{x)dx. Пользуясь кривыми распределения вероятностей, можно производить графические расчеты вероятностей. Например, вероятность попадания величины X в интервал .1X2 (рис. 4-3) равна заштрихованной площади. Вся площадь между осью абсцисс и кривой распределения равна единице. Параметры непрерывных случайных величин. МаГема-тическое ожидание непрерывной случайной величины равно интегралу от произведения ее значений х на плотность распределения вероятностей, причем интеграл берется по всему интервалу возможных значений х:
M = jx<f{x)dx. 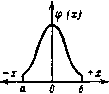 Рис 4-4. Перенос начала координат кривой распределения. Математическое ожидание является центром распределения вероятностей. Если проделать несколько серий испытайий и для каждой из них вычислить среднее значение х, то эти значения будут группироваться вокруг математического ожидания. При симмегричной кривой распределения вероятностей М(х)=а, где а - параметр центра кривой распре- деления (рис. 4-4,а). Если совместить начало координат кривой распределения с центром ее симметрии, то математическое ожидание окажется равным нулю (рис. 4-4,6). Действительно. 6 0 б j лгср {х) dx- - x<f (х)dx-{- j"х<р (х)dx~- 0. а а о Как видно из рис. 4-4,а отклонение случайной величины равно X-а. Как и дискретные, непрерывные случайные величины характеризуются не только математическим ожиданием, но и дисперсией. Дисперсия равна математическому ожиданию квадрата отклонений D\{x - aY<f (л-) dx, а среднее квадратичное отклонение-квадратному корню из дисперсии 3 = /5(x-c)=<p(x)dx , причем интеграл берется по всему интервалу возможных значений л:. Если известно, какому закону распределения подчиняется случайная величина, то достаточно определить параметры М и сг, чтобы иметь полное представленпе о ней. Во многих практических случаях случайная величина подчиняется закону распределения, который сравнительно просто выражается аналитически. Перейдем к рассмотрению некоторых из них. Равномерное распределение. Распределение называется равномерным, если плотность распределения имеет одинаковую величину во всем интервале ее возможных значений (рис. 4-5). Площадь, заключенная между осью абсцисс и кривой распределения, равна единице. Следовательно, Ч{х)2Ь = \ и = Математическое ожидание М= \ л:с?л:?=с, а дис- (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) ( 23 ) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (111) (112) (113) (114) (115) (116) (117) (118) (119) (120) (121) (122) (123) (124) (125) (126) (127) (128) (129) (130) (131) (132) (133) (134) (135) (136) (137) (138) (139) (140) (141) (142) (143) |
|
|