
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) ( 24 ) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (111) (112) (113) (114) (115) (116) (117) (118) (119) (120) (121) (122) (123) (124) (125) (126) (127) (128) (129) (130) (131) (132) (133) (134) (135) (136) (137) (138) (139) (140) (141) (142) (143) (24) Персия а-Ь. Среднее квадратичное отклонение Равномерному распределению подчиняются, например, ошибки глазомерного отсчета части интервала между соседними делениями шкалы прибора. Интервалу 26 соответствует цена деления шкалы. Средняя квадратичная случайная ошибка отсчета составляет около 0,3 цены деления шкалы. У Нормальное распределение. Нормальному закону распределения (распределению o*~~~Zf Гаусса) подчиняется много случайных собы- Рис 4-5. Равномерное раопреде-тий: случайные ошибки леиие. измерений, рассеяние снарядов, отклонения параметров изделий от среднего значения в серийном производстве, срок службы некоторых элементов радиоаппаратуры и др. Установлено, что если отклонения случайной величины вызываются большим количеством независимых случайных факторов и каждый фактор создает лишь небольшое отклонение, то случайная величина подчиняется нормальному закону. Кривая нормального распределения аналитически выражается уравнением (х-а) <р (х) = -тг= е где а - математическое ожидание; а - среднее квадратичное отклонение. 6-244 Нормальное распределение характеризуется следующими свойствами: а) среднее значение случайной величины (математическое ожидание) совпадает с ее вероят-нейшим значением, соответствующим фмакс; б) положительные и отрицательные отклонения равновероятны; в) малые уклонения 0олее вероятны, чем больщие. Математическое ожидание и среднее квадратичное отклонение полностью характеризует случайную величи- 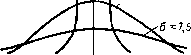 6 =/ Рис. 4-6. Сравнение нормально распределенных случайных величин с разными среднеквадратичными отклонениями. ну, подчиняющуюся нормальному закону. В большинстве практических случаев наибольший интерес представляет изучение отклонений случайной величины от среднего значения (ошибки измерений, рассеяние снарядов и др.). Поэтому часто кривая распределения изображается при а=0, что означает перенос начала координат в точКу х = а. При таком изображении удобно сравнивать различные случайные величины, подчиняющиеся нормальному закону. На рис. 4-6 приведены кривые распределения нормально распределенных случайных величин при разных значениях среднего квадратичного отклонения и а = 0. При уменьшении а кривая сжимается и увеличивается (рмакс- Обычно нужно знать вероятность того, что отклонение случайной величины будет находиться в заданном иитервале значений (вероятность того, что ошиб- ка измерений не превысит заданного значения, вероятность выпуска изделия в заданном допуске на его параметр). Отметим на оси х интересующие нас пределы отклонений случайной величины (рис. 4-7). Вероятность того, что отклонение случайной величины примет одно из значений, находящихся в пределах ±А, равна заштрихованной площади рисунка: Р{~А<х<А)= = --=е Правая часть равенства представляет собой функцию Лапласа Ф (-j, значения которой указаны в приложении 1. Следовательно 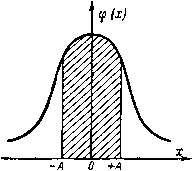 Рис. 4-7. К определению вероятно-сти нахождения случайной величины в допуске ±А. Я{-Л<;с< + Л} = 2Ф(4)- Воспользуемся функцией Лапласа для определения вероятности того, что отклонение случайной величины находится в пределах тЗз. Так как по условию Л = 3з, то Р {-За < X < + За} = 2Ф j 2Ф (3). Пользуясь таблицей приложения 1, находим: Ф(3) = 0,49865 и Я{-35<;c<-f За} = 0,9973. Вероятность того, что отклонение случайной величины будет больше За, определяется как вероятность противоположного события и равна 1-0,9973 = 0,0027. Это значит, что только в одном случае из 370 случайная величина выйдет за пределы За. Мы определили вероятность попадания случайной величины в заданные пределы. Нетрудно решить обратную задачу: по заданной вероятности определить соответствующие пределы изменений х. Найдем срединное от-6» 83 (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) ( 24 ) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (111) (112) (113) (114) (115) (116) (117) (118) (119) (120) (121) (122) (123) (124) (125) (126) (127) (128) (129) (130) (131) (132) (133) (134) (135) (136) (137) (138) (139) (140) (141) (142) (143) |
|
|