
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) ( 26 ) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (111) (112) (113) (114) (115) (116) (117) (118) (119) (120) (121) (122) (123) (124) (125) (126) (127) (128) (129) (130) (131) (132) (133) (134) (135) (136) (137) (138) (139) (140) (141) (142) (143) (26) туры могут оказаться годные. Вероятность того, что при выборочном контроле будут забракованы годные изделия, называется риском поставщика. Риск поставщика и риск потребителя зависят от размера выборки п, т. е. от количества экземпляров аппаратуры, подвергаемой выборочным испытаниям. Чтобы найти связь между результатами выборочных испытаний и числовыми характеристиками всей партии, нужно знать закон распределения проверяемого параметра X, который может быть определен, например, на основании анализа статистических данных испытаний предыдущих партий изделий В массовом производстве распределение параметров изделий часто соответствует нормальному закону распределения. Пусть имеется случайная величина х и известна ее кривая распределения, математическое ожидание М{Х)=а и дисперсия (г. Будем называть а и соответственно генеральной средней и генеральной дисперсией. Пусть экспериментально получены значения х, хи Х2, х, ..., x„. Совокупность этих значений называется выборкой. Выборка характеризуется: выборочной средней х = - {xi+X2 + .. . + Хп); размахом выборки ДГмакс--«мин; выборочным средним квадратичным отклонением Пример 4-19. Имеется 1 ООО сопротивлений. Генеральная средняя этих сопротивлений 10 000 ом. Генеральное среднее квадратичное отклонение 50 ом Известно, что значения сопротивлений распределены по нормальному закону Из этой партии независимо и случайно выбираем 6 сопротивлений. Пусть получена следующая выборка: 9 980, 9 990, 10 020, 9 985, 9 990, 10 000 Выборочная средняя: J = -g-(9 980-f 9 990+ 10020-1- 9 985 -)-9990-f 10000) = 9 994 ом. Размах вцборки: лгмакс - мин = 10)20 - 9980 = 40 ом. Выборочное среднее квадратичное отклонение S=/-L(14« + 4» + 262 + 92 + 4«+6») = i4 8 ом. Оценивая партию изделий по выборочным параметрам, которые мы определили по результатам испытаний небольшой части партии, мы должны знать, насколько отличаются выборочные параметры от генеральных, т. е. от параметров, которые мы получили бы по результатам испытаний такой большой партии, параметры которой а и а можно считать генеральной средней и генеральным средним квадратичным отклонением. Одним из основных способов оценки генеральных параметров по выборочным является определение границ, в которых находятся генеральные параметры (доверительных границ). Рассмотрим применение способа оценки генеральных параметров с помощью доверительных границ для случая нормального распределения. Пусть задан нормальный закон распределения с генеральной дисперсией а. Произведено достаточно много выборок по п членов в каждой. Для каждой выборки получится свое среднее значение: хи Х2, xs, ., Хп- Среднее значение выборок является случайной величиной, которая подчиняется нормальному закону распределения. Можно доказать, что для этой случайной величиныма-тематическое ожидание будет равно а, дисперсия <у{х) = = а/п, а а{х) =a/VДелая только одну выборку из п членов и принимая по результатам ее испытаний, что х = а, мы допускаем некоторую ошибку (рис. 4-11). Отклонение от значения а среднего значения выборки х находится в некоторых пределах ±е. Очевидно, величи- 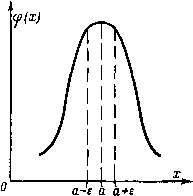 Рис. 4-11. К определению точности выборочной средней. на 8 характеризует точность равенства х=а. Для заданной точности 8 можно найти вероятность того, что среднее значение выборки будет отличаться от а не более чем на 8: a = P{(a-e)<J<(a-f г)} = Величина а характеризует надежность, с которой определяются границы dzs- Пример 4-20. Даны генеральные параметры при нормальном распределении а = 5, о = 1, число членов выборки л = 100. Определить вероятность того, что среднее значение выборки будет отличаться от а не более чем на 0,16. е/л 0.16 Решение. --=-у-.Ш = 1,6. Пользуясь таблицей приложения 1 функции Лапласа, определяем: о =2Ф( 1,6) =.0,89. Задавшись надежностью а, можно определить объем испытаний, т. е. количество изделий выборки п, при котором ошибка 8 не превысит заданного значения. Пример 4-21. а=5, а=1, 8=0,16. Требуется определить размер выборки, при котором среднее значение выборки будет отличаться от а ие более чем на величину 0,16 с надежностью а=0,8. Решение. По условию 2ф У"л = 0,8, Ф У"л = = 0,4. По таблице функции Лапласа находим --- = 1.28. Определяем минимальное необходимое количество членов вы-<j»-1.28a 1.1,28г боркн: л =--=-0Лб5~=5- Если генеральные параметры неизвестны, то можно определить точность выборочной средней по результатам испытаний выборки следующим образом: определяем выборочные параметры из равенств (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) ( 26 ) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (111) (112) (113) (114) (115) (116) (117) (118) (119) (120) (121) (122) (123) (124) (125) (126) (127) (128) (129) (130) (131) (132) (133) (134) (135) (136) (137) (138) (139) (140) (141) (142) (143) |
|
|