Ряд классических методов основан на представлении цепи соединением проходных четырехполюсников или 2х2-полюсников (см. рис. 9). В зависимости от выбора размерности переменных такой проходной четырехполюсник описывают шестью системами уравнений

Л,, л,2

.221 Чг 6,1 Л,.,

21 22

где индексы 1 и 2 входов соответствуют индексам Л и i на рис. 9, а.

Коэффициенты (параметры проходных четырехполюснкх. этих систе.м связаны соотношениями, приведенными в табл. 3.1, где \w\-w,lWa-w,2W2-~ oпpeд.eлиeлъ матрицы параметров. Параметры В-матрицы совпадают с параметрами Л-матрицы при изменении местами номеров входов.

Если индексом 1 обозначен вход, а индексом 2 - выход проходного четырехполюсника, нагруженного на элемент с проводимостью у„=\/Еи (см. рис. 9, б), то

У 22 +У и j/h + ll 22 + гн

2,х -

УиУи + \у\ ZiiZh4-z

- У-П

22+Ун

"21 - -Л21

di, г„ ilz\

У2г + Ун .Vh + II 1+22/н Zii-f-(2(y„ Оп -OijI/h

Традиционный метод анализа заключается в представлении сложной цепи регулярным соединением проходных четырехполюсников с последующим еп; свертыванием к четырехполюснику, эквивалентному цепи на двух ее входах При этом регулярные параллельное (рис. 12, а), последовательно-параллельное (рис. 12, б), параллельно-последовательное (рис. 12, в) и последовательней (рис, 12, г) соединения заменяют одним эквивалентным проходным четырехпи-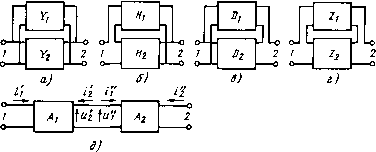

Рнс. 12

люсником, матрица параметров которого равна соответственно сумме матриц У, Н, D или Z соединяемых четырехполюсников. Параметры каскадного соединения (рис. 12, д) определяют произведением =1X2, причем в соответствии с указанными на рис. 9 условными направлениями токов и напряжений знаки параметров оц и «21 при умножении матриц изменяют на противоположные.

Подобный метод не всегда применим, и для свертывания цепи к эквивалентному проходному четырехполюснику используют более общие методы, не связанные с преобразованием параметров. Примером может служить свертывание цепи, описанной матрицей >. к эквивалентному проходному четырехполюснику с матрицей >" по формуле

У.. Ум yki ./22

(3.9)

где миноры Mij равны определителю матрицы Y с вычеркнутыми 1-й строкой и /-М столбцом, а кратный минор Afii,22 - вычеркнутыми первыми и вторыми строками и столбцами.

Временные характеристики цепи, являющиеся оригиналами операторных изображений реакций x{p)F(p)q{p}, находят с помощью обратного преобразования Лапласа, если воздействие можно представить изображением q{p), удовлетворяющим этому преобразованию. В остальных случаях временные характеристики определяют решением дифференциальных уравнений.

Для упрощения расчетов используют нормирование операндов. Простейшее заключается в выборе рабочих размерностей (например, пнкофарад вместо фа рад или килогерц вместо герц), уменьшающих порядок операндов до значений, соизмеримых с единицей. Часто для сокращения числа исходных данных нормирующие коэффициенты (например, С/С„, R/Rn или k-Y/Yg. когда Cn - Clk. L„ = Lk, Ra = Rk) выбирают так, чтобы одна из однородных величии была равной единице. Число коэффициентов степенных многочленов от р уменьшают, деля все коэффициенты на один из них (что не изменяет корней многочлена) и нор мируя р, например р"и = >пр" с подстановкой р = а" ""ря. Дробно-рациональные функции нормируют делением числителя и знаменателя иа один из коэффициентов, что не изменяет значений функции.

В процессе проектирования радиотехнических цепей часто возникает необходимость в составлении расчетных формул с буквенными (символьными) обозначениями параметров матрицы или схемы цепи. Для этого достаточно в формулах, подобных (3,4)-(3.7), разложить Д и .Л,, по символам ненулевых элементов матрицы или схемы.

Напомним, что определитель Д квадратной матрицы А порядка п

2 (-1)*а./,«2/= ... ani„ (3.10)

равен сумме членов, образованных всевозможными произведениями ненулевых элементов Omt матрицы, взятых по одному от каждой строки и каждого столбца, причем знак q-то члена определяется числом инверсий элементов неупорядоченной строки в подстановке индексов 1 2 3 ... п

h /2 3 ... In

Число инверсий б, равно сумме всех больших индексов 1. расположенных перед каждым индексом /,((>!) неупорядоченной строки.

Для разложения определителей по символам элементов матрицы обычно используют теорему Лапласа [4]. Однако этот и другие алгебраические методы разложения определителей громоздки. Межгу тем структура матрицы, как и структура определителей (3.10), полностью определяется множеством индексов ml ненулевых элементов ami матрицы и многие операции над матрицами и определителями можно упростить, используя только Эти индексы и при необходимости индексы составляющих ami. В методе обобщенных чисел [9] структура матрицы отображается матричным числом Рм, каждая строка которого содержит индексы ml ненулевых элементов соответствующей строки матрицы, причем Индекс строки т может быть вынесен за скобки. Если номера строк т упорядочены, то декартово произведение Р (контурное число) элементов / строк матричного числа иад полем модуля 2 равно множеству неупорядоченных строк подстановок членов определителя и однозначно определяет его структуру.

Связь матричного Рм и контурного р чисел с алгебраическим представлением Л определителя описывается формулой

A=detp = det(Pд,)„„2

реализуемой, например, следующим алгоритмом.

1. Представить матрицу матричным числом с п строками.

2. Принять т= 1.

3. Под каждым выписанным элементом / строки т матричного числа провести линию, под которой выписать все элементы (тЧ-1)-й строки, отличающиеся от отделенных линиями верхних элементов.

4. Принять т = тЧ-1.

5. Если т = п, то перейти к шагу 6, иначе к шагу 3.

6. В полученном контурном числе подчеркнуть столбцы (образованные э-1сментами л-й строки и расположенными над ними элементами предыдущих строк, отделенными линиями) с нечетным числом инверсий.

7. Заменить каждый столбец элементов / с учетом номера т строки произведениями элементов a„i матрицы, приписав отрицательный знак членам, соответствующим столбцам с нечетным числом инверсий, и заменив линии, отделяющие несколько элементов /, скобками.

Для разложения миноров Маь-(-1)°+*Да» по этому алгоритму достаточно предварительно вычеркнуть в матричном числе а-ю строку и элементы 1 - Ь.

В качестве примера найдем разложение функций г,х = Ди/А и Ku = \sll\\ по матрице проводимостей

I/,, у,., ООО

.Vai Уг-г Угз О О

О Уз-г Узз Уз* О

О О Уаз Уи Ук

О О О /54 Уъь

Составив матричное число