
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) ( 51 ) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (51) Инструкция. (/о = РО, Л = Р1, У? = Р2, £=РЗ) ерд f/wpg g/O С/П PX=U\ Пример. Для /о= 1,34-10-», Л = 6,5, /?=250 Ом, £=5 В при Um=E, г=1 Ю-з получим {/* =0,41342396 (/«3 мин 20 с). Можно использовать различные модификации метода Ньютона, но необходимость оценки условий сходимости усложняет вычисления н в большинстве случаев вместо этих методов [4, 14] проще использовать рассмотренные методы с гарантированной сходимостью. Эти же методы пригодны и для решения систем уравнений, когда их не удается свести к одному уравнению, но в таких случаях при использовании ПМК с ограниченной емкостью памяти наиболее целесообразным способом решения систем нелинейных уравнений часто оказываются методы нелинейного программирования, рассмотренные далее. 4.3. Анализ нелинейных цепей при гармонических воздействиях В радиотехнике для преобразования спектра сигналов, рассматриваемых во многих задачах как гармонические, широко используют безынерционные (для рассматриваемого диапазона частот) нелинейные цепи. Реакция x(q) такой цепи на гармоническое воздействие q{t)=Acos((i>t-\-(f) будет периодической функцией времени, а составляющие ее дискретного спектра в общем случае определяют формулой (2.2). Эту формулу можно упростить, приняв ф=0. В этом случае в силу четности функции q{t) независимо от вида нелинейности реакция также будет четной функцией, а фазовые сдвиги гармоник ф),=йф прн необходимости можно вычислить после определения спектральных составляющих реакции. Следовательно, x{t)=:-+ Аk cosk(i,i, {4.h\ t, + T 2 r где /4 = - I X (A cos (nt) cos кШШ. t\ При известной характеристике x(q) нелинейного канала передачи сигнала после подстановки q{f)=Acosait коэффициенты Ak (амплитуды гармоник) можно вычислить с помощью одной из базовых программ численного интегрирования, приведенных в гл. 2 илн в [И, 15]. Задача упрощается, если характеристика канала передачи аппроксимирована степенным многочленом x(q) Onq--...- +aii7+ao. В этом случае для вычисления амплитуд гармоник можно воспользоваться формулами .Ко (О =ап. Xl {t)-=an-i+an Acoswt..... *-1 k Xh(t)=an-h + Acos(iit У Л)*cos 1(0/= 2 -4,-*" (~0 < = 0 (4.7) Коэффициенты Л.*этого разложения связаны с полученными на предыдущей итерации коэффициентами Д соотношениями Л*> =а„ ,+ЛЛ(*- )/2, Д<*> =У1 У1<*-> +Л<*- )/2), Л <*) = Л (Л <*- " + /1 ")/2,.... Л{*> = Л (Л ) + Л ))/2..... Л]:*1, =ЛЛ<*Г2>/2, Л(*=ЛЛ ->/2. Прн k=n коэффициенты Л"равны искомым амплитудам гармоник спектра реакции. Описанный алгоритм реализован в следующих программах, отличающихся максимальной степенью аппроксимирующего нелинейность многочлена и способом ввода исходных данных. Программа 179. Вычисление спектра реакции на гармоническое воздействие при аппроксимации нелинейной характеристики многочленом степени пб с коэффициентами ai
Инструкция. (ао=РО, а, = Р1. .... аб=Р6; вместо отсутствующих коэффициентов ввести нули) Л=РХ В/О С/П РХ=РД=Лб, Р7--=Ло. Р8=Л,, Р9 = А2. РА=Лз, РВ=Л4, РС=Лв (/«70 с). Пример. Для x(q)=2q<+lOq+2Qq+\00q+2(Юq+\00Oq-i-l и Л = 4 получим Ло=6081, Л,=15200, Ла=8000, Ла=4800, Л4=2176, Л» 640, Лб=256. Программа 180. Вычисление спектра реакции иа гармоническое воздействие при аппроксимации нелинейной характеристики многочленом степени пЮ с коэффициентами а,- ИПД X П1 С/П ПО ИПД 2 ПС ПД Сх КПС С/П ИП1 ИПД X + ИПО ПО 2 X 2 ПВ КИПВ -f ИПД X ИПВ I - ПВ ИПС - 1 + ХфО 50 « КИПВ КПВ ИПВ 2 + БП 24 КИПВ КПВ ИПД X КПС ипс 1 + ПС БП 10 Инструкция. Л = РД, о«=РХ В/О С/П а„-, = РХ С/П ... а, = РХ С/П а«=РХ С/П РО=Ло, Р1=Л1..... Р9=Л9, РА=Л,„ (/<6Э с). Программа 181. Вычисление спектра реакции на гармоническое воздействие при аппроксимации нелинейной характеристики многочленом степени п12 с коэффициентами
Для проверки правильности ввода н выполиення программ 180 н 181 можно воспользоваться данными примера к программе 179. Прн использовании ПМК с входным языком ЯМК52 можно повысить иа единицу максимальную степень многочлена, соответственно преобразовав программу 181. Прн /110 целесообразно использовать программу 180, а прн пб- программу 179, особенно удобную прн изменении амплитуды воздействия. Рассмотренные программы применимы также для разложения функции cos* а на сумму косинусов кратного аргумента, для чего в исходных данных принять а( = 0, кроме а*=1. Если характеристика x(q) задана таблично или графически, то спектр реакции на гармоническое воздействие можно определить, не вычисляя предварительно ко эффнцненты аппроксимирующего многочлена н воспользовавшись разложением в тригонометрический ряд. Так, при слабой нелинейности функции x(q) с доста точно гладкими участками между пятью равноотстоящими узлами с шагом А/2 коэффициенты первых четырех гармоник н постоянную составляющую в разло женин (4.6) (рнс. 25) можно вычислить по формулам: А„Hx,+xi)-f 2 (xt + x,))/6, Ai = {(x,-xi) + {xt-x,:))/3, A=={(Xi + Xi)~2xi)/4, As = ((xi-Xi)-2 (xt-x))/6, Ai==((xt + Xi)-4(Xt + x) + 6xs)/\2. По вычисленным амплитудам гармоник вычисляют и коэффициент гармоник 1 V/ 2 /4* 4 .используемый обычно для оценки нелинейных искажений. 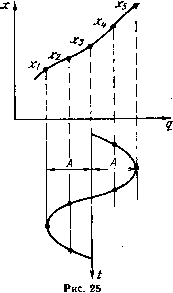 (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) ( 51 ) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|