Пример. Для Л, = 5,43656 X Х10-2 А/В; Л2 = 2,18743-10-б А; а, = 10 В-, 02 = 6,493498 В-; при {7о=0,2 В, 8 = 0,01, АС=0,05

получим (/«3 мии 45 с) IgmalH

= 7,3033252-10-3 См «7,3 мСм, С* = 0,202, Д[/* = 0,0004.

При решении многих задач удобно контролировать ход минимизации функции, прекращая вычисления по достижении границы оптимума (неполный координатный спуск) и выбирая Ах в зависимости от результатов вычислений. В этом случае длина базовой части программы минимальна. Что существенно при минимизации сложных функций, фрагмент вычисления которых занимает значительную часть программной памяти П.МК

Программа 196. Минимизация функции Ф(х) методом неполного координатного спуска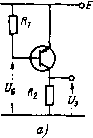

Рис. 27

ИП7 ИПЗ + П8 ... 00 ИП9 С/П БП 00

П9 - х<0

Инструкция. Заменить миоготочие фрагментом вычисления Ф(х) при х=Р% и использовании регнстюв, кроме 7, 8 и 9; Ф(Х1,) или Ы0"=Р9, *в=Р8, Дл;о=Р7 В/О С/П РХ=Р9=Ф(л;1), P8=a;i, Дх:,=Р7 СД1 РХ = Р9=Ф(л;2), Р8= = JCj ... Дл:,--1 = Р7 С/П РХ=Ф(х:0. P8=JCi, P7=A:i-i вычисления прекращать при достижении минимума Ф(х) с требуемой точностью.

Для примера рассмотрим использование неполного координатного спуска для расчета статического режима в цепи с включением транзистора по схеме с общим коллектором (рис. 27, а). Так как в рассматриваемой схеме обычно Лб<Л1 и exp(A(t/g3 - /gB - кэ))* соответствии с уравнениями биполярного транзистора (4.5) для рассматриваемой цепи значение бэ °" ределяется решением уравнения

E~Ri(cz-d)-R(az-\-b)-U=Q, где а = 11 (\-a.Na,);

* = «/ко/("~°ла/); с=(1-алг) /до/С -a.va/);

d= (\-а,) 1о/(\~ама.1); г = ехр (ACg). Минимизируя квадрат иевязки этого уравнения, определим t/gg, а затем /3= = 02+6, /5 =cz-d, UlRi, UE-IRi (см. рнс. 27,а).

Программа 197. Расчет статического режима цепи с биполярным транзистором, включенным по схеме с общим коллектором

ИП7 ИПЗ + П8 ИПЗ X е" 1 - П4 ИПА X ИПВ + П5 ИП2 х ИП4 ИПС х ИПД - П6 ИП1 X -f ИПЗ + ИПО - х2 ИПЭ П9 - 7«0 00 ИПЭ С/П ИПО

ИП1 ИП6 X - ИП5 ИП2 X С/П

Инструкция. (£ = Р0, «i = Pl, 2 = P2, Л = РЗ, а = 1Ц1 -«лга/) = = РА, 6=а ко/(1~ала/)=РВ, с = (1-адг)/эо/(1-°лга/) = PC. d={l --ал)/ко/(1-«Ла/)=РД) 1-)0«» = Р6, A(/) = P7, (7°э = Р8 В/О С/П РХ = = Ф, Р8 = (/Уз, PTAfy*", Л(/*> = Р7 В/О С/П РХ = Ф ... Д(/-"Р7 В/О

С/П РХ = Ф (иД) Р8=(/э, Р7 = Л( С/П РХ = (/э, PY = [/б, Р. = /б, Р5 = /э.

Пример. Для £--=10 В, «i=100 кОм, 2=1 кОм, Л=39 В", 0 = 10"* А, , = 4-10- А, с = 2.10- А, d=1.10- А при 110"«=Р9, (Уэ* = О, AU = 0,05 получим (/ибо с) (/У = 0,25 В, Ф= 1738,89; при Л(/=- 0,01 получим {tx ~60 с) Ф = 6,2040597, (/=0,2 В; при Л{У = 0,002 получим (/=«60 с) Ф = = 1,023617, (/[;э=0,21 В; при Л(/ = -0,0004 (/«60 с) Ф = 0,012088, U = = 0,2072 В; при Л(/=0,00008 (/«60 с) Ф = 0,0000394, (/ = А(/) В; при Л(/ = - 0,000016 (/ « 90 с) Ф = 0,0000004, (/> = (0,207472 ± AU) В; {Уэ = 3,268 В, (/б = 3,474 В; = 0,065 мА, 1 = 3,268 мА.

Затраты времени иа решение оптимизационных задач уменьшаются при рациональном выборе начальных значений оптимизируемых переменных и стратегии поиска оптимума. В связи с простотой программной реализации метода равномерного последовательного поиска его целесообразно использовать и при одномерном поиске оптимума нескольких переменных иа каждой итерации. Простейшие методы нелинейного программирования [tl7J основаны иа одномерном поиске минимума вдоль координатных осей (координатный спуск) или по направлению аитиградиента, соответствующего направлению максимального уменьшения функции (скорейший спуск). При использовании методов скорейшего спуска необходимо вычисление производных минимизируемой функции, которая должна быть аналитической. Это требование отпадает при координатном спуске, наиболее приемлемом для программирования микрокалькуляторов. В этом случае число операций уменьшается при определении иа каждой итерации граиипы оптимума последовательно для каждой переменной с последующим автоматическим изменением шага Ах=-Ах/а. Траектория поиска оптимума при таком неполном координатном спуске напоминает спираль.

Программа 198. Минимизация функции Ф(Х{, Xi) двух переменных методом спирального координатного спуска

ИП7 ИП8 + П8 ПП 27 х<0 00 ИП7 ИПО + П9 ПП 27 х<0 08 ИП7 /-/ а - П7 х2 ИП5 - х<0 00 С/П ... ИПб Пб - В/О

Инструкция: Заменить многоточие фрагментом вычисления Ф{Х1, Xi} при Xi = P8, Х2=Р9 с использованием регистров, кроме 5, .... 9 (е/аР=Р5, М099=Р6, Ал:=Р7, л:1 = Р8, х:2=Р9 В/О С/П РХ= (Ах*/а) = {г/а)\ Р7 = Ах*,

Р8 = л:;, Р9 = л:*, Р6 = Ф(л:;, х*).

Пример. Целевую функцию Ф (х, jtj) = (дс+j:2 -1))+(i + «2 - 7) используют [17] в качестве тестовой для сравнения качества различных алгоритмов нелинейного программирования при исходном векторе переменных Хо= [1 1], что приводит к оптимуму Л*= [3 2] с минимумом функции Ф(Х*) =0. При той же исходной точке (8/3)2 = 2,5-10" н а = 3 по программе 198 получим для этой функции Ф(Х*) = 1,87361 10- л:* =2,99994, л:2 = 1,99994 приблизительно за 11 мии.

Полностью автоматизированный поиск оптимума методом спирального спуска применим только для достаточно гладких и выпуклых [17] в области оптимума функций. Существенные трудности возникают при минимизации функций нескольких переменных с крутыми оврагами - вытянутыми областями равных уровней функции в пространстве переменных с резким возрастанием функции по обе стороны от оси оврага. При минимизации овражных функций, как и функций общего вида с недостаточно исследованными свойствами, целесообразно автоматизировать только поиск границ оптимума каждой переменной методом неполного координатного спуска с последующим выбором оптимизируемой переменной и ее приращения (шага поиска) в зависимости от полученных ранее результатов.

Программа 199. Минимизация функции Ф{х1, х) двух переменных методом неполного координатного спуска

ИП7 ИПЗ + П8 ПП 20 х<0 00 ИП9 С/П ИП7 ИП9 + П9 ПП 20 х<0 10 БП 08 ... ИП6 v> П6 - В/О

Инструкция. Заменить миоготочие фрагментом вычисления Ф(х1, Xi) при xi-PS, Х2=Р9 с использованием регистров, кроме 6...9; Ы0" = Р6, Ах=Р7, Xi = PB, Х2=Р9; для оптимизации переменной Xi выполнять В/О С/П РХ=Ф{хи Х2), P8=x(i) ,Дл:=Р7 В/О С/П для оптимизации переменной Х2 после xi выполнять С/П PX=*(*i, Х2) P9=x<.i\ Ах=Р7 С/П при начале оптимизации с переменной Х2 выполнять БП 1 О С/П РХ=Ф{хи хг), Р9=л:>, Ах==Р7 С/П ...

После каждого выполнения этой программы определяется граница оптимума выбранной цеременной, которую можно уточнить, уменьшая и изменяя знак шага, или перейти к оптимизации другой переменной в зависимости от вычисляемых значений Ф{Х1, хг). Поиск прекращают после достижения минимума с требуемой точностью.

Среди тестовых функций, используемых для сравнения качества алгоритмов минимизации овражных функций [17], наиболее известна функция Розеиброка Ф(хи X2) = l()0{x2-X2)+(l-Xi) с изогнутым крутым оврагом, минимумом Ф(Х*)=0 прн Х*=[1 1] и началом поиска минимума из точки Х°=[-1,2 Г], Прнмеиеине программы 199 для миинмизацни этой функции обеспечивает достаточно быстрый спуск к точке минимума вдоль крутого оврага [15], Следует отметить, что классические методы скорейшего и координатного спуска ие обеспечивают минимизации функции Розенброка вследствие «ацикливаиия» поиска иа «дие» крутого оврага прн достижении локального минимума, В то же время при иеполиом координатном спуске точки поиска расположены иа склонах оврага, что обеспечивает продвижение вдоль оси к минимуму,