
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) ( 57 ) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (57) тем принять Д=-Д, выполняя В/О ... В/О ... В/О ... на отрезке /?>о>-Л, ш = Я и С/П ... С/П ... С/П ... на отрезке о = -Л, /?>о)>0. После определения интервалов, в которых изменяется знак (например, 1тА{р) при Re/l(p)>0), следует спуститься вдоль соответствующих линий равного уровня фо до кория, уменьшая Д по мере уменьшения абсолютных значений ЯеА{р) и \тА{р). Найденные таким образом корни могут быть определены с погрешностью, определяемой лишь операционными ошибками вычисления ReA(p) и Im А(р). Максимальную степень многочлена А(р) можно увеличить иа 2 при использовании ПМК с входным языком ЯМК52, соответствеиио изменив программу 201 [11]. Метод неполного координатного спуска применим и для оптимизации функций большего числа переменных, ограничиваемого лишь емкостью памяти ПМК. Примером мижет служить следующая программа. Программа 202. Минимизация функции шести переменных методом неполного координатного спуска ИПО ИП1 + П1 ПП 54 х<0 00 С/П ИПО ИП2 + П2 ПП 54 х<0 09 С/П ИПО ИПЗ + ПЗ ПП 54 х<0 18 С/П ИПО ИП4 + П4 ПП 54 х<0 27 С/П ИПО ИП5 -f П5 ПП 54 х<0 36 С/П ИПО ИП6 -f П6 ПП 54 х<0 45 С/П .., ИПД ПД - В/О Инструкция. Заменить в программе миоготочие фрагментом вычисления целевой функции Ф(х) при Xi = PI, ;t2=P2, ;te=P6 с использованием при необходимости регистров 7, 8, С; л"=Р1, х = Р2, Хд = Р&, Ах=РО, М0««=РД; для оптимизации В/О С/П; для оптимизации переменных в порядке номеров для достижения одной границы нажимать С/П; для раздельной оптимизации Xj нажимать БП О 9 С/П, для Хз - БП 18 С/П, для х4 - БП 2 7 С/П, для xj - БП 3 6 ,С/П, для хв - БП 45 С/П; после каждого выполнения программы РД = Ф(Х"*), Р1 = x\K Р2 = х*, .... Р6=х<). Пример. Минимизировать функцию шести переменных [17] /6 \ / 6 Ф (X) = ехр Xi] П Xi \i=4 / / ; = 1 с ограничениями Xi>0 и оптимумом Х*= [1 2 3 4 5 6]. Заменим миоготочие в программе 202 фрагментом вычисления заданной функции ИП1 ИП2 + ИПЗ + ИП4 + ИП5 + ИП6 + е" ИП1 ИП2 х2 ~ ИПЗ f X - ИП4 х2 х2 ИП5 t х2 X -г ИП6 х2 t х X -f- При Jt =х1 =...=х1 =Ах = 0,1 на первом витке спирального спуска (при пуске программы нажатием клавиш В/О С/П ... С/П ... С/П ... С/П ... С/П ... С/П .„) получим (время первого выполнения программы около 190 с, последую- щих - около 190 kc, где k - номер переменной) Ф = 3,3103895• 10"*, х,= 1,1, \х2 = 2,1, Хз = 3,1, 4 = 4,1, Х5 = 5,1, Хб = 6,1. Прн выборе для следующих витков спирального спуска Ах = -0,02; 0,005; -0,001 после четвертого витка получим ф(Л-*) =3,2716195-Ю-" при Л-*= [0,999 1,999 2,999 3,999 4,999 5,999. Если фрагмент вычисления целевой функции прн использовании рассмотренных базовых программ не вмещается в свободной части программной памяти, то достаточно автоматизировать только вычисление целевой функции с изменением переменных перед каждым пуском программы в соответствии с предыдущими результатами, регистрируемыми в вычислительном бланке. В таких случаях также наиболее удобен координатный спуск. Следует отметить, что рещение задачи методами нелинейного программирования связано со значительными затратами времени. Поэтому такие методы целесообразно использовать лищь в том случае, когда рещение задачи не может быть найдено другими способами с меньшими затратами времени. 4.5. Расчет временных характеристик нелинейных цепей Анализ нелинейной цепи с инерционными компонентами в динамическом режиме сводится к рещению нелинейного дифференциального (неоднородного при ненулевом значении воздействия) уравнения. Точность рещення таких уравнений численными методами зависит от порядка выбранного метода и величины щага интегрирования Л = /,-Прн малом шаге для исследования процессов на заданном отрезке времени приходится выполнять больше вычислений, что приводит к увеличению затрат времени и возрастанию операционной составляющей погрешности результатов вычислений. При большом шаге возрастает методическая погрешность и вероятность неустойчивости вычислений, при которой вычисляемые величины изменяются периодически илн скачкообразно вне связи с физическими условиями задачи. Во избежание неустойчивости вычислений и обеспечения сходимости вычислительного процесса (зависящей и от выбора начальных условий) шаг интегрирования следует выбирать таким, чтобы в течение этих интервалов времени Л = /,-/,-i процессы в анализируемой цепи и независимое воздействие отображались монотонными и достаточно гладкими функциями. Выбор порядка численных методов решения дифференциальных уравнений [4, 14, 15, реализуемых, в частности, с помощью базовых программ 150-152, определяется требуемой точностью решения, допустимыми затратами времени и сложностью дифференциального уравнения, ограничиваемой емкостью памяти ПМК. В качестве иллюстрации рассмотрим переходные процессы в последовательном соединении резистора с сопротивлением R, идеального источника напряжения e = e(t) и полупроводникового диода. Представляя диод параллельным соединением идеальной модели с характеристикой i = /o(eu i) где u = u{t) - напряжение на диоде, и нелинейной емкости С = С(и) =у1 + ау\+ \и\ с барьерной и диффузионной составляющими, можно описать анализируемую цепь уравнением е-и-/?(i+ic) =0, где ic==dC(u)u/dt= (C+udC/du)du/dt. Следовательно, переходные процессы в рассматриваемой несложной цепн описываются относительно громоздким дифференциальным уравнением {e-u)/R-i dt у/„((1+Л) exp(Au) -1 +a Vl+uP + aP/2 Vl+«p Для приближенного решения этого уравнения целесообразно использовать метод Эйлера, реализованный программой 150. Так как правая часть составленного уравнения явно не зависит от времени, то при составлении рабочей программы для сокращения времени счета целесообразно вместо вычисления текущего времени использовать счетчик числа шагов (например, согласно КИП6). Программа 203. Вычисление напряжения u(t) и тока i(t) инерционного днода ИПЭ - ИП2 ~ ИПЭ ИП1 X е" - ИПО X V ИП4 X ИПО ИП1 X ИПЗ ИП5 X X ИПЭ + ПЗ - ИПЗ ИП4 X ИПЭ X» 1 + / ПВ 2 ИП5 X ИПА X + ИПЭ X + ИПЗ ИПВ X + - ИП7 пэ КИП6 ИП6 ИП9 С/П БП 00 Инструкция, (/о = РО, А = Р1, = Р2, а = РЗ, Р = Р4, V=P5) Л=Р7, и„ = РЭ, О = Р6, е„ = РХ В/О С/П РХ = «i, PY = 1, Р8 = ij, = РХ С/П ... е„ = РХ С/П РХ = РЭ = Un, PY = Р6 = л, Р8 = i„ (/«17 с). Ярилер. Для /„=1,3 10~ А, А =6,5 В~, У? = 100 Ом, « = 510 Р = Э5 В"", v= 10" Ф/А прн Л = 510~2 с, «« = 0, = 1 получим «=0,001; 0,0018783; 0,0026658; 0,0040431; 0,00465714 В; i.-= 0; 8,47256 10-; 1,596059-10-5; 2,272231-10- 2,890004-10- А; . .. При использовании метода Эйлера для уменьшения погрешности приходится выбирать весьма малый шаг, что приводит к значительным затратам времени на решение задачи. Поэтому в общем случае целесообразно использовать методы более высокого порядка, например усовершенствованный метод Эйлера- Коши второго порядка, реализованный базовой программой 151. Для примера исследуем процесс опрокидывания триггера иа туннельном диоде (рис. 29, а) при пренебрежении влиянием емкости диода, значительно меньшей внешней емкости С. Временные характеристики рассматриваемой цепи отображаются уравнением i-(£-и) ?,-(Мз-u) ?2-f-C(du/d/) =0 илн du/d/= ((«з-«) ?2 + 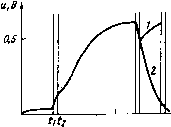 200 tj и % t,MC 6) (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) ( 57 ) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) |
|
|