dui/dT = p (iBx -/„ (exp (Л («1-Uj)) -1)-Ui/Q;

dijdx--=.ujp- dujdxaplo (exp (Л ("i-u))- 1)-«»/(Wp C„),

где p= yZTC; (? = <0p ЛС; <Op=--l/VZr; a = C/C„ и безразмерная независимая переменная т = <Ор/.

При использовании метода Эйлера необходимо выбрать достаточно малый шаг, что приводит к существенному увеличению объема вычислений. Поэтому введем в рабочую программу фрагмент со счетчиком шагов, обеспечивающим вывод результатов вычислений после заданного числа шагов. В связи с этим один из параметров (например. Л) будем вводить в текст программы и ограничимся случаем совпадения частоты воздействия с резонансной частотой контура (Ор.

Программа 206. Анализ переходных процессов в настроенном амплитудном детекторе

ИП6 ИП9 - ИП2 X t 2 3 О + х<0 15 Сх БП 17 е 1 - ИП1

X t ИПД X ИПА X ИП9 ИПС - -

ИП7 X ИП9 + П9 -- ИПЗ + ИПЗ ИП5 X sin ИП4 X 1-» - ИПА X ИП6 ИПВ

- ИП7 X ИП6 + П6 Вх ИПА ~ ИП7 X ИПЗ 4- ПЗ ИП7 ИПЗ + ПЗ ИП9 L0 00 С/П БП 00

Инструкция. Установить переключатель Р-ГРД-Г в по.тожение Р; Л= Р7, /о = Р1, Л = Р2, /вх =- Р4, ш/шр = Р5, р = РА, Q = РВ, а)рЛ„С„ = PC а = РД, = РЗ, Р6, = Р9, число шагов « = РО (после каждого

выполнения программы сохраняется Р0= 1) (В/О) С/П (/«20 с) РХ = Р9 = и*2. PY = РЗ = Xi = То ~Ь /Л, Р6 = и.\\ РЗ =

Пример. Для /„ = 10~ А, А = 39 1/В, /вх = 0,2-10~ А, ш/шр =1, р = = 1000 Ом, Q = 10, (йр/?оС„ = 100, а = 0,1; Л = я/50, т„ = и" = = = = 0 получим uSpQ; 0; 0; 6,28.10-; 1,88.10"" u*,"«0; 7,89-10"*;

2,7510-; 4,69-10- 7,78-10~3; .,..i[>«0; 0; 4,9510-*; 1,97-10"; 4,92х

Х10~"; ... . Результаты вычислений приведены на рис. 32.

В рассмотренной задаче резкое изменение экспоненциального члена прн увеличении входного напряжения заставляет выбирать очень малый шаг интегрирования для уменьшения методической погрешности, что приводит к значительным затратам вре.мени и увеличению операционной составляющей погрешности результатов вычислений. Их точность можно повысить, выбрав метод интегрирования более высокого порядка, но этот выбор существенно ограничен малой емкостью памяти ПМК. Среди методов второго порядка достаточно экономичным относительно затрат ресурса памяти на базовую часть программы является модифицированный метод Эйлера [i5] с вычислениями по формулам

4+)=40+ft/,(; + ft/2, х<Ч /2,..., 4")-

*=1, 2..... n; i = 0, 1, 2, ...

На микрокалькуляторе с входным языком ЯМК34 этим методом можно решать системы, содержащие до пяти уравнений простейшего вида, но при решении практических задач число уравнений н их слож. ность также ограничены ресурсом памяти.

Программа 207. Решение системы из четырех дифференциальных уравнений Xi = fk(t; X....., д:4) модифицированным методом Эйлера

ИП4 П8 ИПЗ П7 ИП2 ПП 37 4 2 X П9 ИП4 ИП8 П4 *-* П8 ПЗ П7 ИП2 ИПб П2 ПП

П9 + ПО ИПЗ П1 С/П Пб X ИП4 + П4 ... ИП9 X ИПЗ . .. ИП9 X ИП2 + П2 ... ИП9 + П5 ИПО ИП9 В/О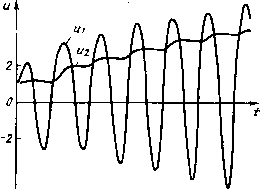

Рис. 32

ПО ИП9 ИПЗ ИП7 37 2 . . . ИП9

+ ПЗ X ИП1

Инструкция. Заменить многоточия фрагментами вычисления соответственно функций ft, /..,, /j при t = РО, Xj = Р5, Хг = Рб, Хз = Р7, Х4 = Р8 с использованием регистров памяти, кроме О ... 9; /i/2 = Р9, /„ = РО, xj* Р! = = Р5, xf > = Р2, хР = РЗ, xf = Р4 В/О С/П РХ = Р1 = х{", Р2 = х", РЗ = = -4", Р4 = х\ РО = /„ + Л В/ОС/ПРХ=... В/О С/П РХ=Р! = х<", Р2 = =х<2 P3=.v, Р4 = х<,>, PO=/„ + i/i.

Пример. Для системы уравнений х, = Xj, Xj = .<з, Х3 = Х4, х = I-24xj-- 50x2 - 35хз - !0Х4 при /„ = О, = О, .4° = 2, х!," = -4, х*," = 2, /i=0,01 получим (/«45 с): х*/= 0,0198; 0,039202033 ; 0,058208464; ...; х, (О,!) = = 0,18040512; х2=!,960!; 1,9204207; 1,8809812; ...; х. (0,1) = i ,6129905,

=-3,97895; -3,9559266; -3,9310499; ...; .«3 (О, I) =-3,7140956; .4= = 2,2036; 2,3949359 ; 2,5745189; ...; Х4 (0,1) = 3,5416507.

Программа 207 при решении системы с числом уравнений, меньшим четырех, соответственно сокращается, а ресурс памяти для записи уравпенкй увеличивается. При небольшом числе уравнений можно использовать методы интегрирования третьего или четвертого порядка, но в последнем с."уме удается реализовать решение систем, содержащих не более двух уравнений [15].

Решение дифференциальных уравнений п-го порядка в норм :.,ьмой форме

d"x/d/"=/ (/; X, х, X".....х<"-*)

подстановками Xi=x, Х2=х[, Хз=х2- Хп-х сводят к решению системы из п дифференциальных уравнений первого порядка xlx, х2=Хз, х„ у =

=г.Хп, x„ = f(t, Xl, ...,Хп)-

В этом случае для решения дифференциального уравнения п-го порядка можно использовать программы, подобные программе .207, причем требования к ресурсу памяти снижаются, так как достаточно обеспечить вычисление х а определение правых частей остальных уравнений сводится к вызову из памяти значений соответствующих переменных. Дополнительное увеличение ресурса памяти, остающегося после ввода базовой программы, обеспечивается использованием комбинированного метода второго порядка [!5], реализованного следующей программой, результаты выполнения которой имеют несколько большую операционную погрешность, чем вычисленные по программе ,207.

Программа 208. Решение дифференциального уравнения четвертого порядка x=f(t; X, х, х", х") комбинированным методом второго порядка

ИП4 П5 ПП 36 ПП !2 ПП 36 + ПП !2 С/П П4 ИПО ИП9 + ПО ИП5 ИП9 х ИПЗ + ПЗ Вх ИП9 X ИП2 П2 Вх ИПЭ X ИП! + П1 В/О ... ИПЭ X t ИП5 + В/О

Инструкция. Заменить многоточие фрагментом вычисления функции /(/; Xl, х, Хз, Xf) эквивалентной системы уравнений первого порядка при /=Р0, a;j = P1, Xj = Р2, Хз = РЗ, Xj = Р4 с использованием регистров, кроме О, 5, 9; Л/2 = Р9, /„ = РО, х(/о) = Xi(/„) = PI, х(о) = хСо) = Р2, х"(<о) = Хз(/о) = = РЗ, х"(о) = 4(h) = Р4 В/О С/П РХ = х(/о + Л) С/П РХ = х(/„ + 2Л) ... С/П РХ = Р! =х(/в + 1Л), Р2 = х(/„ + /Л), РЗ = х"(/„+(Л), Р4 = х"(/о+ ), РО = = /i = /„ + ih.

Пример. Для уравнения xi-f-!Ox"-f35x"-f50х-ь24х= I, представив его системой уравнений, приведенной в примере к программе 207, при х,(0)=х(0) = = 0, Х2(0)=х(0)=2, х»(0)=х"=-4, Х4(0)=х"(0)=2, Л = 0,01 получим (/«35 с): x(/i) = 0,0199; 0,039401; ,..; х(0, I) =0,18133588. Точное значение х(0, 1) =0,180489 определяется аналитическим решением х= 1-е--1-2е-- -Зе-з(+е-<.

Если правая часть дифференциального уравнения явно не зависит от переменной /, то программы 20i7 и 208 можно несколько сократить, заменив, например, вычисление текущих значений ti вычислением числа шагов (выполнений программы). По образцу программ 207 нли 208 составляются рабочие программы для решения дифференциальных уравнений третьего или второго порядка. В последнем случае достаточно точное решение обеспечивает метод Рунге - Кутта четвертого порядка.

Программа 209. Решение уравнения x"=f{t, х, х) методом Рунге-Кутта четвертого порядка