Отсюда после интегрирования

Из формулы (1.97) видно, что, когда модуляции нет (Аи) = 0), текущая фаза изменяется по линейному закону <f=wot+<fo-

При частотной модуляции, когда Аю Ф О, текущая фаза высокочастотного колебания непрерывно изменяется относительно значения юо-Ьфо- Это изменение происходит по синусоидальному закону

с амплитудой """"" и частотой модулирующего сигнала.

Из рис. 1.122 видно, что в положительный полупериод модулирующего сигнала частота, а следовательно, и фаза ЧМ колебаний увеличиваются. Поэтому в положительный полупериод модулирующего сигнала ЧМ колебания опережают по фазе колебания несущей частоты (колебания при отсутствии модуляции), а в отрицательной - отстают от них.

Амплитуда изменения фазы (девиация фазы) при частотной модуляции Дфмвкс называется индексом частотной модуляции. Индекс частотной модуляции прямо пропорционален девиации частоты и обратно пропорционален величине модулирующей частоты. Индекс частотной модуляции обозначим т/..

% -Фмакс --Q---р-I

где -/макс - 2« - 2« •

Если модулирующий сигнал не является однотонным, а состоит из колебаний различных частот, то в формулу (1.98) для определения индекса модуляции должно входить макси.мальное значе-нпе модулирующей частоты -Рмакс:

Д/ыакс

mf~-p-.

Как видно из форму.пы (1.97), при частотной модуляции одновременно с изменением частоты изменяется и фаза высокочастотных колебаний, т. е. частотная модуляция всегда сопровождается фазовой модуляцией.

Однако, несмотря на то, что девиация частоты и девиация фазы связаны прямо пропорциональной зависимостью (Ди)макс = = 0Д9макс), ФМ сигнал и ЧМ сигнал нельзя отождествлять. Действительно, при сложном модулирующем сигнале девиация частоты зависит не только ог девиации фазы, но и от частоты модулирующего сигнала. При фаз.овой модуляции в соответствии с передаваемым сигналом изменяется фаза несущих колебаний (девиация фазы пропорциональна амплитуде модулирующего сигнала). Получающуюся же при фазовой модуляции девиацию частоты нельзя считать пропорциональной амплитуде модулирующего сигнала,

так как связывающий девиацию частоты и фазы коэффициент пропорциональности Q изменяется в процессе модуляции.

Поэтому, например, прием ФМ колебаний на приемник, предназначенный для приема ЧМ колебаний, практически невозможен без предварительного преобразования фазовой модуляции в частотную. Для такого преобразования можно использовать интегрирующую цепь RC. Напряжение иа вы.ходе такой цепи связано с напряжением на входе соотношением

•-вых- I-i- -вх»

или при R- пренебрегая вторым слагаемым в знамена-

теле.

Из формулы (1.99) следует, что амплитудно-частотная характеристика интегрирующей цепи Л (й) обратно пропорциональна частоте сигнала

/C(Q) = = -.

Поэтому если модулирующий сигнал в фазовом модуляторе пропустить через интегрирующую цепь RC, то девиация частоты при фазовой модуляции перестает зависеть от частоты модулирующего сигнала, т. е. ФМ сигнал превращается в частотно-модулированный. 1

Фазовая модуляция для радиосвязи не применяется, однако использование фазового модулятора с интегрирующей цепью является довольно распространенным способом получения ЧМ колебаний.

2. Спектр частот ЧМ сигнала

Исходя из формул (1.97) и (1.98) и полагая для простоты начальную фазу 90 = 0, выразим ток в антенне прп наличии частотной модуляции:

г А == COS 9 = COS (шо -f Vlf %ш Ш). (1.100)

Определим спектр колебаний при однотонной модуляции (при Q = const). Раскрыв скобки в выражении (1.100) по известным тригонометрическим формулам, получим

гд == [cos cos {rrif sin 9Л) - sin wt sin (тsin Qt)]. (1.101)

Разложение сложных функций cos (my sin и sin (my sin Q) в ряд Фурье возможно только с помощью так называемых функций Бесселя:

cos {Ttif sin GO = Л {mj) + 2Л {Щ) cos 2Qt + 27 (m) сое AQt +...; sin {nif sin Qt) = 21 (/re) sin Ш + 2/s (/и) sin 3/ + ...

Подставив в выражение (l.IOl) эти ряды и используя известные тригонометрические формулы для косинуса суммы и разности двух углов, получим

«А = У О (%) COS + Л (m/)COS (Шо -h ) - -/i (%) COS(o)o - Й)-Ь

-Ь л (/«/) COS (о)о -f 2S) -Ь 72 (/И/) cos (юо - 22) -f ... (1.102)

Во всех выщеприведенных формулах множители типа /„(ту) являются математическими функциями Бесселя п-го порядка. Графики функций Бесселя различного порядка показаны на рис. 1.123.

Зп 1т f)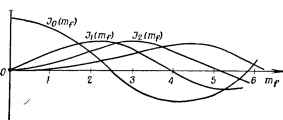

Рис. I.I23. Графики функций Бесселя

Как видно ИЗ этого рисунка, значение функции нулевого порядка 1о(т) максимально при индексе модуляции ту=0. Функции J\(inf), Ji{mf), laimj) и т. д. приобретают максимальные значения при различных индексах модуляции. Отсюда следует, что спектр ЧМ сигнала содержит бесконечный ряд колебаний боковых частот, амплитуды которых являются функциями индекса модуляции. На практике при определении ширины спектра принято учитывать только боковые частоты, амплитуды колебаний которых составляют более 5% амплитуды колебаний несущей частоты.

На рис. 1.124 показаны спектры ЧМ колебаний при различных индексах модуляции ту. Как следует из рисунка, при ту<1 спектр ЧМ сигнала имеет ширину около 2/макс, так как заметную амплитуду имеют лишь колебания первой пары боковых частот. Такая частотная модуляция называется узкополосной. Недостатком узкополосной частотной модуляции является плохое качество воспроизведения сигнала, поэтому для радиовещания используется широкополосная ЧМ, т. е. модуляция при значениях индекса модуляции, равных о- 8.

Ширина спектра частот, занимаемого ЧМ сигналом, при широкополосной модуляции может быть приближенно оценена удвоенным значением девиации частоты 2А/ыакс.