Ом в квадрате (см. § 3.43), то входное сопротивление дуального двухполюсника равно k/Z{p). Нули дуального двухполюсника, являющиеся полюсами исходного, также должны быть расположены в левой части плоскости р.

Из курса математики известно, что если имеются два кратных корня уравнения N(p) - 0, то соответствующие им слагаемые в решении берут в виде (Cj + С2/)е. Если допустить, что на мнимой оси могут быть два кратных корня р = /Р, то соответствующая им свободная составляющая (Cj -}- С2/)е нарастала бы до бесконечности, чего физически быть не может. Коэффициенты аиЬ е числителе и заменателе Z(p) должны быть положительны. Если бы это условие нарушилось, то на основании леммы, вытекающей из теоремы Гурвица (см. § 17.2), среди корней уравнения Z{p) = О появились бы корни с положительной действительной частью.

Поясним, почему степень т не может отличаться от степени более чем на единицу. Допустим, что степень т больше степени п на два. Тогда р-оо является нулем второй кратности для Z{p\ а то, что происходит при р->-оо, можно считать происходящим на мнимой оси плоскости р (мнимая ось простирается в бесконечность). Но тогда на мнимой оси получается кратный корень, чего быть не может.

Проведя такое же рассуждение для дуального двухполюсника, убедимся, что степень п не может быть больше степени т более чем на единицу.

Если в Z{p) вместо р подставить /ы, то Z(/(o) будет представлять собой комплексное сопротивление двухполюсника в установившемся синусоидальном режиме при частоте со, а ReZ(/o)) - действительную часть входного сопротивления. В том случае, когда двух-

полюсник содержит резистивные сопротивления, его ReZ(/G))>0(oH потребляет активную мощность /ReZ(/G))]. Если же двухполюсник

чисто реактивный, то ReZ(/(o) = 0. В общем случае для пассивного двухполюсника всегда должно быть ReZ(/co)0.

В литературе по синтезу цепей иногда пользуются термином «положительная действительная (вещественная) функция». Под ней понимают функцию: 1) действительная часть которой положительна, если положительна действительная частьр; 2)действительная при действительном (не комплексном) р. Поскольку Z(p) этим свойствам удовлетворяет, оно является положительной действительной функцией.

Пример 111. Задано несколько выражений вида М(р)/М{р). Выяснить, могут ли - они представлять собой входные сопротивления некоторых двухполюсников:

I) 5р-6 20р-Ь12р + 6

25р2 4- 12р + 2 Up" -f 8р + 12р2 + 13р -Н Г

Sp-bp+l 2р-р+1

р-Ьр + р-Ь1 (р+1)(р2+1)"

Р е ш е н и е. Первое выражение не может представлять собой Z(p), так как один из коэффициентов в числителе отрицателен. Второе и третье выражения также не могут представлять собой Z{p): второе потому, что максимальная степень р в знаменателе больше максимальной степени р числителя на два, третье потому, что

3/7 -Н 1 -f 1 1 (1 -о))(1 -2о)2) 1- 0)2)2(1 +0)2)

+ + Р + 1

при значениях о) от 0,707 до 1 отрицательно. Четвертое выражение всем требованиям удовлетворяет и потому может представлять собой Z(p) некоторого двухполюсника.

Кроме названных общих свойств перечислим свойства Z(p) двухполюсников, состоящих только из /? и с, только из /? и L и только из L и с. Двухполюсники типа RC и RL имеют чередующиеся простые нули и полюсы на отрицательной вещественной оси плоскости р. Для /?С-двухполюсников ближайшей особой точкой к началу координат является полюс, в бесконечности полюс отсутствует. Для двухполюсников типа RL ближайшей к началу координат особой точкой является нуль, при р = 0 полюс отсутствует. Двухполюсники типа LC имеют чередующиеся простые нули и полюсы на мнимой оси. Степени полиномов числителя и знаменателя отличаются на единицу.

Нули и полюсы Z{p) можно изобразить условными значками из комплексной плоскости, скажем, нули кружками, полюсы крестиками. Полученную картину называют картой нулей и полюсов. Эта карта наглядно характеризует частотные свойства двухполюсника и реакцию его при воздействии единичного напряжения.

По расположению и количеству нулей на ней можно определить число апериодических и колебательных компонент, которое содержит свободная составляющая, и быстроту затухания той или иной из них во времени. Чем ближе к мнимой оси расположены нули, тем медленнее затухает соответствующая им свободная составляющая.

Существует несколько способов реализации двухполюсников по заданной Z(/?), удовлетворяющей перечисленным в§ 10.2 условиям. Три основных способа реализации рассмотрены в § 10.3 - 10.5.

§ 10.3. Реализация двухполюсников лестничной (цепной) схемой. Познакомимся с понятием непрерывной дроби. Непрерывной называют дробь вида

d+...

Входное сопротивление или входная проводимость лестничной (цепной) схемы по типу рис. 10.1, а, в которой продольные сопротив-

е с т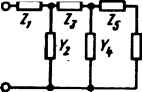

f d п a)

3f8 30/3SJ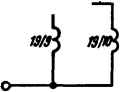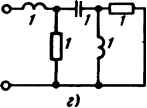

Рис. 10.1

ления названы Zj, Z3, Zg,a поперечные проводимости - Fg. 4.

могут быть представлены непрерывной дробью.

Для того чтобы убедиться в этом, проделаем небольшие выкладки. Найдем входную проводимость правой части схемы по отношению к зажимам тп. Она равна Суммарная проводимость

правой части схемы по отношению к зажимам тп с учетом ветви с проводимостью F4 равна У44- \ , .Входное сопротивление поот-

ношению к тем же зажимам

Входное сопротивление всей схемы равно

(10.2)

Z,4-

Таким образом, возникает задача о переходе от (10.1) к (10.2), т. е. задача о последовательном упорядоченном определении элементов лестничной схемы (Z,, Zg, У2» 4» 6» ••) по выражению (10.1). С этой целью:

1) располагаем полиномы N{p) и М{р) по убывающим либо по возрастающим степеням р\

2) делим многочлен на многочлен, следя за тем, чтобы в процессе Деления получались положительные (не отрицательные) слагаемые и чтобы они не содержали р в степени больше 1 и меньше - 1;