Пример 115. Реализовать Z{p) - ---

Решение. Прир=0 у Z(p) нет полюса, поэтому последовательно включенный конденсатор у искомого двухполюсника отсутствует. Функция Z(p) имеет два полюса Pj2=±/, расположенных на мнимой оси. Выделим параллельный резонансный контур рис. 10.2, 0, соответствующий этим полюсам:

= Res Z(p) == Res

рЧр+2р

Зр+2р+1 0)= 1; 1/(0)2)= 1 Гн.

-3+2/+1 2 2ауь

Найдем функцию минимального реактивного сопротивления:

Z,{p)Z{p)-

В соответствии с рис. 10.2, г реализуем Zj(p) в виде параллельного соединения 7=1 Ом и L-\ Гн. Схема искомого двухполюсника изображена на рис. 10.4, б.

Двухполюсники, состоящие только из /? и С, могут быть реализованы, например, канонической схемой рис. 10.4, б, а состоящие из и L - схемой рис. 10.4, г. Для схемы рис. 10.4, в

rffe = limZ(p); = limpZ(p); b, = ResZ(p).

k p-*-oo ->-0 p=-df

Для схемы рис. 10.4, г

= limZ(/7); Ц = \[mZ{p) /р.

Параметры R, и находим, имея в виду, что сопротивление соответствует параллельному соединению R, и L, где

= т, = R, /Lk\ = ResZ(p) /р.

§ 10.5. Метод Бруне. Основные этапы метода Бруне следующие.

1. Прежде всего проверяют, не содержит ли заданное Z(p) [назовем его Zзaд(p)l полюсов на мнимой оси. Если они имеются, то из состава Z (р) выделяют соответствующие этим полюсам один или несколько последовательно включенных параллельных резонансных контуров. В результате получают

2а,р (10.5)

зад(Р)-1-Г = ад- Р2+«

Этот этап соответствует переходу от рис. 10.5, а к рис. 10.5, б.

о с jt Л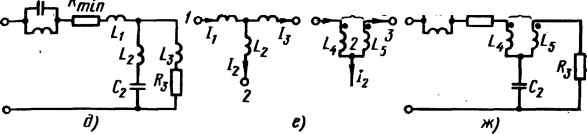

Рис. 10.5

Коэффициент = Не52ззд(р). Функция Z{p) не имеет полюсов на мнимой оси и

р = /cofe

представляет собой функцию минимального реактивного сопротивления.

2. Полагая р == ]\о в Z(/(d) выделяют действительную часть, т. е. находят Re Z{j(o) и определяют частоту со, при которой Re = ReZ(/ci)) минимальна. Эта частота может быть равна нулю, бесконечности или иметь некоторое конечное значение (в последнем случае ее будем называть wq). Подсчитывают также минимальное значение ReZ(/ci)), которое называют

3. Из Z{p) вычитают Ri и находят Z{p). Этой операции соответствует переход от рис. 10.5, б к рис. 10.5, в. Заметим, что степени числителя и знаменателя Zy{p) одинаковы.

4. Если частота, при которой имеет место минимум ReZ(/ci)) равна нулю или бесконечности, то уже на этой стадии делается попытка реализовать Z(/7) лестничной схемой. Если же минимум ReZ(/ci)) имеет место при некоторой со = coq, отличающейся от О и оо, то дальнейшую реализацию производят в соответствии с п. 5 - 12.

5. Подсчитывают Zj(p) при /? = /со. Так как при частоте р = /coq действительная часть Z{p) = то действительная часть разности Z(/coq)-равна нулю, т. е. Z,(/(0(j) представляет собой чисто реактивное сопротивление jX.

6. Возможны два случая. Первый, когда Jfi>>0, второй, когда Л,<:0. Будем полагать Л, = coqL,>0 (случай Jfj<0 рассмотрен в п. 12). Тогда

L, = XJiOQ. (10.6)

7. Составляют разность Z,(p)-pL, и приводят ее к общему знаменателю. Например, если исходить из того, что

p+b,p+bQ

то проводимость оставшейся для реализации части двухполюсника

рЛ-ЬрЛ-Ьд

Zx{p)-pLi -pL-\-pH\~bL)-{-p(a-bQL)+af;

Обратим внимание на то, что в знаменателе Yq{p) имеется слагаемое -pL,

JOTopoe при дальнейшей реализации приведет к появлению в схеме отрицательной "ИДуктивности.

8. Поскольку при р = /со, Z,(p)-pLj=0, то Yjip) == оо, т. е. р = /coq является болюсом Yq{p). Наличие полюса у Kq(p) позволяет представить оставшуюся часть

двухполюсника ветвью из последовательно соединенных и С2, настроенной в резонанс на частоту Uq, и параллельно ей присоединенного двухполюсника сопротивлением Zp){pHc. 10.5, г):

P/L I (10.7)

/7+0)5 2(/7)

9. ПолагаютZ2(/7) = Np) / Мр).Степени полиномов Nip)Mip)цолжны быть

такими, чтобы после приведения правой части (10.7) к общему знаменателю степень полинома числителя левой части равнялась степени полинома числителя правой части; то же и в отношении степеней знаменателей. Так, если Yp) соответствует выражению (а), то Z2{p) == (cjP+Cq) / d.

Методом неопределенных коэффициентов можно найти Cj, Cq, dQ и В рассматриваемом случае

с, = -/,0)2; Cq = Uq, dQ = bQ, (10.8)

L2 = ZjWo / {bo-iol); C2 = 1 /

Разность (&o-Wq)>0; это следует из того, что условие Aj>0 означает, что

>0, а при р = /(Oq ReZj(/7) = 0.

L 10. Реализа-11ию Zp) производят, как правило, лестничной схемой. В рассматриваемом примере Z2(p) реализуют индуктивным L- - с / dQ = -WqL, / bvi резистивным /?3=aQ/&o элементами (рис. 10.5, д). Важно обратить внимание на то, 4T0L3 оказалось отрицательной.

11. Так как физически осуществить отрицательную L3 в линейной цепи невозможно, то дальнейший этап реализации в методе Бруне состоит в том, чтобы три магнитно не связанные индуктивные катушки, имеющие индуктивности Lj, L2 и L3, заменяют трансформатором, состоящим из двух катушек L4 и L5, между которыми имеется магнитная связь (взаимная индуктивность М). Это действие является обратным по отношению к операции "развязывания" магнитно-связанных цепей.

На рис. 10.5, е изображены два участка цепи: левый - до преобразования, правый - после преобразования; показаны положительные направления токов в ветвях и указаны одноименные зажимы катушек. Напряжения между точками / и2 для обоих участков цепи в силу из эквивалентности должны быть одинаковы, т. е.

/7L,/,+pL2/2 = pLI-pMI, -PL2/2+PV3 = pLIs-pMI.

Подставляя в эти две строки /i=/24-3 и учитывая, что каждая из них должна удовлетворяться при любых значениях токов, получают:

М = L4 = L, + L2; 5 = 2+3 (109)

где La и Lb положительны. Окончательная схема изображена на рис. 10.5, ж.

12. Если условиться сумму степеней полиномов в числителе и знаменателе зад(/) называть порядком ZJp), то совокупность перечисленных операций ("цикл Бруне") позволяет снизить порядок на четыре. Естественно, что потребность в каком-либо одном или нескольких этапах в любом конкретном примере может и не возникнуть (например, в этапах 1 или 3).

Для Zзgд(/7), порядок которых достаточно высок, может возникнуть потребность применить эту последовательность операций не один раз. В заключение отметим, что если в п. 5 Х,<;0, то L,<;0, а вычитание согласно п. 7 сопротивления - р \ 1[сводится к прибавлению сопротивления -\-р

Некоторым недостатком метода Бруне является его относительная сложность и необходимость введения в схему идеального трансформатора с коэффициентом связи k = М" / {LL) = 1.