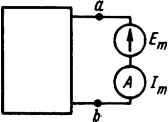Рис. 2.16

рить ток в /п-ветви, вызванной ЭДС Е. Частное от деления тока /п-ветви на ЭДС /п-ветви и дает g.

Выделим /п-ветвь, обозначив всю остальную часть схемы (не содержащую ЭДС) некоторым прямоугольником (рис. 2.16). Вся схема, обозначенная прямоугольником, по отношению к зажимам аЬ обладает некоторым сопротивлением. Его называют входным сопротивлением. Входное сопротивление /п-ветви обозначим /?вхт-Тогда

R..m = / = 1 / = А / А,,. (2.11)

Таким образом, входное сопротивление /п-ветви есть величина, обратная входной проводимости этой ветви. Его не следует смешивать с полным сопротивлением /п-контура в методе контурных токов.

Пример 15. Определить входную gn и взаимную g\2 проводимости в схеме рис.

2.13.

Решение. Контуры в схеме рис. 2.13 выбраны так, что ветвь / (ветвь сЬт) с источником ЭДС fj входит только в первый контур, а ветвь 2 (ветвь со) с источником ЭДС £2 - во второй.

Поэтому можно воспользоваться определителем системы Д и алгебраическими дополнениями А,, и Ajg, составленными поданным примера 13:

25 1009

1009

0,025Ом- = 0,025См,

0,081Ом- =0,081См.

§2.16. Теорема взаимности. Теорема взаимности формулируется следующим образом: для любой линейной цепи ток в k-ветви, вызванный источником ЭДС Е, находящимся в т-ветви, /ft = Eg равен току в т-ветви, вызванному источником ЭДС Е (численно равной ЭДС Е), находящимся в Л-ветви, / = Egf.

Для доказательства теоремы взаимности обратимся к рис. 2.15,а. Как и при выводах в § 2.15, выделим две ветви схемы: ветвь k

Рис. 2.17

И ветвь т. Включим в ветвь т источник ЭДС £", в ветвь k - амперметр А для измерения тока Пусть каждая из ветвей /гит входит соответственно только в /г- и т-контуры. Поэтому по методу контурных токов= ЕА I Л. Поменяем местами источник ЭДС и амперметр, т. е. источник ЭДС переместим из ветви т в ветвь k и назовем теперь а амперметр - из ветви k в ветвь т. В этом случае ток

= Amk I А-

Так как £,

А в силу симметрии определителя

системы А относительно главной диагонали (см. § 2.13), то ток / в схеме рис. 2.15, б равняется току в схеме рис. 2.15, в.

При практическом использовании теоремы взаимности важно иметь в виду взаимное соответствие направлений токов и ЭДС в схемах рис. 2.15, б,в.

Так, если ЭДС £ источника ЭДС, находящегося в /г-ветви схемы рис. 2.15, е, направлена согласно с контурным током / в схеме рис. 2.15, б, то положительное направление отсчета для тока в схеме рис. 2.15, в будет совпадать с положительным направлением контурного тока по ветви т (ЭДС Е в схеме рис. 2.15,в направлена по /).

Для нелинейных цепей теорема (принцип) взаимности невыполнима. Цепи, для которых не выполняется принцип взаимности, называют необратимыми.

Пример 16. В схеме рис, 2.17 переключатели Pi, Р% Рз и Рл могут находиться в первом или во втором положении. Если они находятся в положении /, то в схеме включен только один источник ЭДС £4. Под действием ЭДС £4 протекают токи /i = = 1,5 А, /2 = ЗА, /з = 1А. Найти ток U, если все переключатели находятся в положении 2, полагая, что Е\ = 20 В, £2 = 40 В, £3 = 50 В, £4 = 10 В.

Решение. Для определения тока /4 воспользуемся принципом наложения и принципом взаимности. Если бы в схеме был включен один источник ЭДС £j = 10 В,

Амперметр включаем только для наглядности; сопротивление амперметра полагаем равным нулю.

Рис. 2.18

а остальные (Eg и £3) отсутствовали, то в ветви 4 по принципу взаимности протекал бы сверху вниз ток в 1,5 А. Так как ЭДС £, = 20 В, то в ветви 4 протекает ток, равный 1,5-20/10 = 3 А. Аналогичным образом найдем токи в ветви 4 при включении источников ЭДС 2 и " произведем алгебраическое сложение частичных токов (с учетом их направления):

=T + To-To=•

§ 2.17. Теорема компенсации. Рассмотрим два варианта этой теоремы. В любой электрической цепи без изменения токораспре-деления сопротивление можно заменить: 1) источником ЭДС, ЭДС которого численно равна падению напряжения на заменяемом сопротивлении и направлена встречно току в этом сопротивлении; 2) источником тока У, ток которого численно равен току в этом сопротивлении и имеет то же направление, что и ток /.

Для доказательства теоремы компенсации выделим из схемы одну ветвь с сопротивлением R, по которой течет ток /, а всю остальную часть схемы условно обозначим прямоугольником (рис. 2.18,а).

Если в выделенную ветвь включить два одинаковых и противоположно направленных источника ЭДС Е, ЭДС которых равна падению напряжения на сопротивлении R под действием тока I {Е = =IR; рис. 2.18,6), то ток / в цепи от этого не изменится. Убедимся, что разность потенциалов между точками а и с в схеме рис. 2.18,6 при этом равна нулю. Действительно,

/RE=:ip-IR~\-lR

Фс=Фа

Если = фд, то точки а и с можно объединить в одну, т. е. закоротить участок ас и получить схему рис. 2.18, в. В ней вместо сопротивления R включен источник ЭДС Е.

Схема, соответствующая второму варианту теоремы, изображена на рис. 2.18, г. Чтобы прийти к ней, заменим последовательно соединенные RuE на участке ас (рис. 2.18, б) параллельным соединением источника тока У = E/R = I и сопротивления R. Так как

Номер ветви соответствует индексу ЭДС.