„ 1 ар Idp „

т. е.совокупностью условии --- = О,--- = О и т. д. 1 ак как вторые производные

2 оц)у 2оц>2

1 дР 1 дР

- -- - G, ,>-0, - -г = G99>-0 положительны, то это и является доказательством

2 dq>\ 2

минимума тепловой функции р.

Пример 23, Найти токи в ветвях схемы рис. 2.24 и сделать проверку по второму закону Кирхгофа. Дано: £41 = 10 В; £14" = 6 В; £12" = 20 В; £21" = 30 В; £31 = 14 В; £24= 10В;£43 = 8В;£2з"= 12В;£з2 = 7В;/?41= 10м;/?14" = 20м;/?12= ЮОм; /?21" = 5 Ом; /?31 = 2 Ом; /?24 = 4 Ом; /?34 = 2 Ом; R23," = 4 Ом; = 2 Ом. Источник тока, включенный между узлами 3 и2, дает ток /32 = 1,5 А.

Решение. Записываем систему уравнений:

Ф,С1, -f Ф2С,2 + 4>3i3 = Ju-

ф,С2, + Ф2С22 + Фз23 = -22; Ф1Сз1 + ф2Сз2 + ФзСзз = 33.

Подсчитываем проводимости:

G22=

41 14" 12 1 1 1

R. "

21 21 <33 = ~ + +

21" 31

1 1 1

+-+-+

23"

G,2 = G01 = -

23" 1

13=31 = - =

24 R3I

+--=1,75См;

2,4 См; 1,4 См;

43 1

R "

= - 0,4 См;

0,5 См;

G23 = G32 = - (0.25 + 0,5) = - 0,75 См.

При подсчете G22, G33 и G23 учтено, что проводимость ветви с источником тока равна нулю (сопротивление источника тока равно бесконечности).

Узловые токи:

£ "

£iL fii "~/?4,"~/? "

£.

31

31 12

= 15А;

F " 23

•22 - о / D 32 23

Г) / о ii t<l2 K21

+ Уз2=- 1.5А;

/33 == 3,5 + 3 - 7 + 4 - 1,5 = - 5 А.

Система уравнений

2,4ф, - 0,4ф2 - 0,5фз = 15;

- 0,4ф1 + 1,4ф2 - 0,75фз= - 1,5;

- 0,5ф, - 0,75ф2 + 1,75фз = - 5 имеет решение ф, = 6 В; фз = 0,06 В; Ф3 = - 1,07 В.

Заключительный этап расчета состоит в подсчете токов по закону Ома. Перед определением токов в ветвях схемы следует эти токи обозначить и выбрать для них положительные направления:

£4/-(Ф1-Ф4) 10 (6-0)

~ /?4l ~ 1 ~

Ф2 ~ Ф1

ФЭ - Ф2 + , Ф4 - ФЭ + 43

V =--= Аз =-Б- А и т. д.

32 43

Сделаем проверку решения по второму закону Кирхгофа для периферийного контура.

Алгебраическая сумма падений напряжений 4-1 + 1,1855 - 2,92-2 - -4,55-2 ж - 5 В.

Алгебраическая сумма ЭДС 10 - 7 - 8== - 5 В.

Покажем, что основная формула (2.20) метода двух узлов получается как частный случай (2.22). Действительно, если один узел схемы (рис. 2.23), например узел 6, заземлить, то остается найти только один потенциал - 1),. Для получения формулы (2.20) из (2.22) следует положить ф, = ф = и;, фд = фз = Ф4 = ... =0.

§ 2.23. Преобразование звезды в треугольник и треугольника в звезду. Соединение трех сопротивлений, имеющее вид трехлучевой звезды (рис. 2.25), называют звездой, а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рис. 2.26), - треугольником. В узлах /, 2,3 (потенциалы их ф, и фз) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).

Обозначим токи, подтекающие к узлам /, 2, 3, через /,, /3 и /3.

Часто при подсчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема «не заметит» произведенной замены. Выведем формулы преобразований. С этой целью выразим токи /, /2 и /3 в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.

Для звезды

/1 -Ь /2 -Ь /з = о, (2.23)

/, (ф, - ф),; /2 = (фз - фо)2; /3 = (фз - ф)з. (2.24)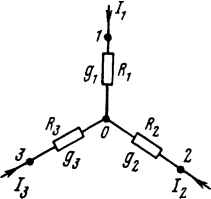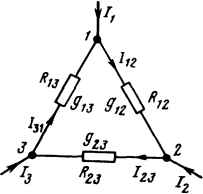

Рис. 2.25

Рис. 2.26

Подставим (2.24) в (2.23) и найдем ф:

Ф11 4- Ф22 4- Фзз - Фо(1 4- 2 4- з) = О,

откуда

Ф11 + Ф2Я2 + Фзз

§1+2 + Яз

Введем ф в выражение (2.24) для тока 1{.

1Ф1(Я2 + ei) - Ф2Я2 - Фзёз!

•1 +2 + Яз

(2.25)

(2.26)

Для треугольника в соответствии с обозначениями на рис. 2.26

/,=/,2-/з,=(ф1 -Ф2)Я12-(ФЗ-Ф1)Я13=Ф1(12+Я1з)-Ф3Я13-Ф2Я12- (2.27)

Так как ток /, в схеме рис. 2.25 равен току /, в схеме рис. 2.26 при любых значениях потенциалов ф,, Ф3, то коэффициент при фд в правой части (2.27) равен коэффициенту при фз в правой части (2.26), а коэффициент при фз в правой части (2.27) - коэффициенту при Фз в правой части (2.26).

Следовательно,

12 = gigJiex 4- 2 4- 3); (2-28)

gigJigi 4- g2 4- з)- (2-29)

Аналогично,

23 = g2gj(gx 4- 2 4- з)-

(2.30)

Формулы (2.28) - (2.30) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды. Они имеют легко запоминающуюся структуру: индексы у проводи-мостей в числителе правой части соответствуют индексам у прово-