(3.29)

dt с

Запишем его в комплексной форме: Вынесем за скобку:

R + /Чо/. -

Следовательно, для схемы рис. 3.9

(3.30)

(3.31)

Это уравнение позволяет найти комплексную амплитуду тока через комплексную амплитуду ЭДС и сопротивления цепи coL и l/wC.

Метод называют символическим потому, что токи и напряжения заменяют их комплексными изображениями или символами. Так, Rl - это изображение или символ падения напряжения iR\

JdiLI - изображение или символ падения напряжения Ui = L-; --1 - изображение или символ падения напряжения на конден-

саторе J idt.

§3.12. Комплексное сопротивление. Закон Ома для цепи синусоидального тока. Множитель R + /wL - (j/ioC) в уравнении (3.30) представляет собой комплекс, имеет размерность сопротивления и обозначается через Z. Его называют комплексным сопротивлением:

I (3.32)

Z = 2eJ* = /? + /toL -

ti)C

Как и всякий комплекс, Z можно записать в показательной форме. Модуль комплексного сопротивления принято обозначать через Z. Точку над Z не ставят, потому что принято ставить ее только над такими комплексными величинами, которые отображают синусоидальные функции времени.

Уравнение (3.30) можно записать так: IZ = Е. Разделим обе его части на д/2 и перейдем от комплексных амплитуд и £ к комплексам действующих значений / и Е:

i = E/z. (3.33)

Уравнение (3.30) представляет собой закон Ома для цепи синусоидального тока.

В общем случае Z имеет некоторую действительную часть R и некоторую мнимую часть jX:

Z = R + jX, (3.34)

где R - активное сопротивление; X - реактивное сопротивление. Для схемы (см. рис. 3.9) реактивное сопротивление

X -=- (oL - 1 /соС.

§ 3.13. Комплексная проводимость. Под комплексной проводимостью У понимают величину, обратную комплексному сопротивлению Z:

Y=\/Z = g- 1Ь = уе-. (3.35)

Единица комплексной проводимости - См (Ом~). Действительную часть ее обозначают через g, мнимую - через Ь. Так как

1 1 7,

Z R-\-iX jjx R-X R + X

=FT *=FT = - (3.36)

Если X положительно, то и положительно. При X отрицательном b также отрицательно.

При использовании комплексной проводимости закон Ома (3.33) записывают так:

l=UY, (3.33а)

или

f=Ug- jUb = -h

( где /ц - активная составляющая тока; - реактивная составляющая тока; и - напряжение на участке цепи, сопротивление которого равно Z.

I § 3.14. Треугольник сопротивлений и треугольник проводимостей. Из (3.34) следует, что модуль комплексного сопротивления

Z = RX\ (3.37)

Следовательно, z можно представить как гипотенузу прямоугольного треугольника (рис. 3.10) - треугольника сопротивлений, один катет которого равен R, другой - X. При этом

tg9 = X/R. (3.38)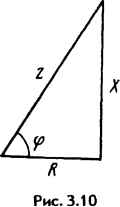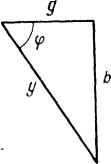

Рис. 3.11

Аналогичным о6\к\ юм ж)дуль комплексной проводимости в соответствии с (3.36) у = g + Ь- Следовательно, у есть гипотенуза прямоугольного треугольника (рис. 3.11), катетами которого являются активная g и реактивная b проводимости:

tgф = b/g.

(3.39)

Треугольник сопротивлений дает графическую интерпретацию связи между модулем полного сопротивления z и активным и реактивным сопротивлениями цепи; треугольник проводимостей - интерпретацию связи между модулем полной проводимости у и ее активной и реактивной составляющими.

§ 3.15. Работа с комплексными числами. При расчете цепей переменного тока приходится иметь дело с комплексными числами: сопротивление участка цепи или цепи в целом - это комплекс; проводимость - комплекс; ток, напряжение, ЭДС - комплексы. Для нахождения тока позакону Ома нужно комплекс ЭДС разделить на комплекс сопротивления.

Из курса математики известно, что комплексное число можно представить в

трех формах записи: алгебраической а + показательной се* и тригонометрической ссо5ф + jcsirnp.

Сложение двух и большего числа комплексов удобнее производить, пользуясь алгебраической формой записи. При этом отдельно складываются их действительные и мнимые части:

(«I + + («2 + /*2) + («3 - /з) = («1 + «2 + «з) + /(1 + 2 - *з)-

Деление и умножение комплексных чисел целесообразно производить, пользуясь показательной формой записи. Например, нужно разделить комплекс Cje*i на

комплекс Cges. В результате деления будет получен комплекс

сеП = --= - е<*1 ~ *2)

С2е"»2 С2

Модуль результирующего комплекса равен частному от деления с, на С2, а аргумент Фз = Ф1 - Ф2-

При умножении двух ком[1лексов Cie*** и С2е*2 результирующий комплекс

При расчетах электрических цепей часто возникает необходимость в переходе от алгебраической формы записи комплекса к показательной или наоборот.