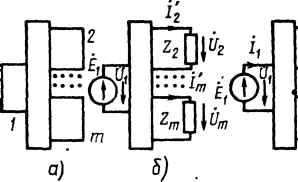
Рис. 4.16

принципа наложения запишем выражения для токов ветвей:

-Л = 111 - 212 - 313 - ••• - иУ, Ч = \У2\ - 2У22 - 323 - •• - 1тУ2т

V= flf/ml - 2m2- 3

mifmrrf

Изменим направления токов в ветвях 2 - m на противоположные и назовем их токами /2 - /,д(/2 = - h\ im = - /т)(рис. 4.16, г). Для того чтобы все слагаемые уравнений имели положительные знаки, введем следующие обозначения; Ykk = ykk,

У Ik =-yik=- ykv Ypr = Yrp = V -УгрРгфХ).

Тогда система уравнений многополюсника (а) будет иметь вид

mifi=i/i;

Если систему уравнений многополюсника (б), записанную в К-форме, решить относительно [U], то получим систему уравнений многополюсника, записанную в Z-форме:

[U] = [Z][I],

IZ] =

-11 12 21 22

Z-mX Zm2

Чт 2m

Если у многополюсника Ykm ф Ymk, его называют невзаимным. Если многополюсник содержит источники энергии (активный автономный многополюсник), тоего уравнения в Y- или Z-форме запишутся подобно тому, как это сделано в § 4.16 д.я четырехполюсника: ,

[ У ] [ (}] = [/ - /, J ил и [Z1 [/ - = (Щ.

Исследование работы электрических цепей часто проводят графическими методами путем построения круговых и линейных диаг-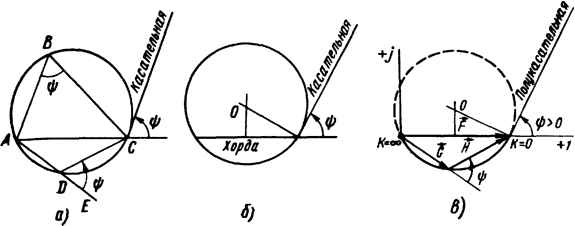

Рис. 4.17

рамм. Перед тем как приступить к изучению круговых диаграмм, рассмотрим вопрос о построении дуги окружности по хорде и вписанному углу.

§4.18. Построение дуги окружности по хорде и вписанному углу.

Из курса геометрии известно, что вписанным углом называют угол, вершина которого находится на окружности, а стороны являются хордами.

Вписанный угол измеряется половиной дуги, на которую он опирается. Так, ZABC =-\\) (рис. 4.17, а) измеряется дугой ADC/2, а ZADC - Ауто\\АВС/2. Сумма ZABC -\-ZADC =п.

Угол Z£DC дополняет до л угол Zl/IDC, поэтому ZJEDC =\.

Какое бы положение ни занимала точка D в интервале от А до С, угол между продолжением хорды AD (т. е. линией DE) и хордой DC остается неизменным и равным ф.

Угол между продолжением хорды АС и касательной (полукасательной) к окружности в точке С также равняется углу -ф. d-i Центр окружности О находится на пересечении перпендикуля-"ра к середине хорды и перпендикуляра к касательной (рис. 4.17, б). / Из изложенного следует, что если заданы хорда и вписанный угол "Ф, то для нахождения центра окружности необходимо: 1) восставить перпендикуляр к середине хорды; 2) под углом ф к продолжению хорды провести прямую, которая будет являться касательной к окружности; 3) восставить перпендикуляр к касательной; пересечение перпендикуляра к хорде и перпендикуляра к касательной даст центр окружности.

§ 4.19. уравнение дуги окружности в векторной форме записи.

Построения, аналогичные построениям рис. 4.17, а, могут быть выполнены и на комплексной плоскости. В этом случае все хорды, например СА, DA, CD, являются векторами.

На комплексной плоскости рис. 4.17, в совместим хорду

СЛ = f с осью + 1. Если угол ф >0, то от продолжения хорды его

откладывают против часовой стрелки; если -ф <0, угол откладывают по часовой стрелке.

Обозначим DA =G и CD = Я. Тогда

- - - (4.31а)

Вектор Н опережает вектор G на угол -ф. Пусть модуль вектора Н будет в k раз больше модуля вектора G. Тогда

H=kGe.

(4.316)

Если k = 0,то И - О и G = F. При k = оо И = F и G = 0. Подставив (4.316) в (4.31а), получим

G{ 1 + ke") = F,

G=F/{i -{-kei").

(4.31в)

Уравнение (4.31b) называют уравнением дуги окружности в векторной форме записи.

При изменении коэффициента /г от О до с» меняются оба вектора

G и Я, но так, что угол ф между ними остается неизменным, а сумма векторов равна вектору F. Конец вектора G скользит по дуге окружности, хордой которой является вектор F. Поэтому можно сказать, что дуга окружности является геометрическим местом концов вектора G.

Рабочей частью окружности, или рабочей дугой, является та часть окружности, которая по отношению к хорде лежит по обратную сторону от полукасательной (рабочая дуга на рис. 4.17, в вычерчена сплошной линией, нерабочая - пунктиром).

Рабочая дуга меньше половины окружности при <90° и больше половины окружности при ф >90°.

§ 4.20. Круговые диаграммы. Из § 3.4 известно, что синусоидально изменяющиеся функции времени (токи, напряжения) могут быть изображены векторами на комплексной плоскости. Если процесс в электрической цепи описывается уравнением, по форме тождественным уравнению (4.31в), то геометрическим местом концов вектора тока (напряжения), выполняющего в уравнении электриче-