Решение, с помощью табл. 7.1 запишем разложение трапецеидальной ЭДС:

4-220 1

=-(sinlO°sinw< + - sin30°sin3w< +

+7 sin50°sin5w< + sin70°sin7a)0-Zo 4У

Следовательно,

вА = 274sinw< -f 89,3sin3a)< + 49,5sin5a)/ + 30,9sin7w

По нулевому проводу протекает только третья гармоника тока

/ - L

-03 ~г -нЗ/З

где £з=89,3/л/2=63,3 В; 2оз=1,5/; 2„з=6 4/; 2„ / 3 = 2 - /1,33; /оз = 63,3 / / (1,5 + 2 - /1,33) = 31,8 е~ А. Мгновенное значение тока /цз = 44,8sin(3o)/ - 4°40) А.

§ 7.14. Биения. Колебательный процесс, получающийся в результате сложения двух синусоидальных колебаний с равными амплитудами Л и близкими, но не равными частотами ш, и (02, дает колебание, которое называют биением. Пусть f{t) =v4sino),/ +i4sinw2/.

Воспользуемся известным тригонометрическим преобразованием

„ а - р а + р sma -- sinp = 2cos--- sin -~-.

Следовательно, /(/) можно представить следующим образом: , f{t) =2/lcosQsino),

где Й =(о), - (Og) / 2, (О =((0, +0)2) / 2(2 <с:со).

График результирующего колебания изображен на рис. 7.13. Амплитуда колебания изменяется по закону 2i4cosQ/. Огибающая колебаний нанесена пунктиром.

Возникновение биений при сложении двух синусоидальных колебаний с равными амплитудами и близкими (но не равными) частотами используется на практике в различных целях, в частности для того, чтобы установить, что складываемые колебания имеют неодинаковые частоты.

§7.15. Модулированные колебания. При передаче информации Широко применяют модулированные колебания. Модулированным колебанием/(О =Asin{oit называют колебание, в котором амплитуда Л, частота со, фаза я)? или и те и другие вместе изменяются во времени.

Колебание, в котором изменяется только амплитуда Л, а угловая частота со и фаза ф неизменны, называют колебанием, модулированным по амплитуде.

Огидающая

(D-i2 а>+£2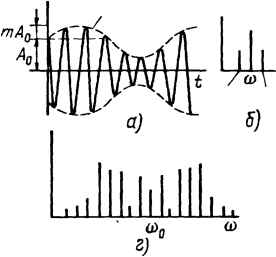

Рис. 7.14

Колебание с изменяющейся угловой частотой со, но неизменными амплитудой А и фазой ф, называют колебанием, модулированным по частоте.

Колебание, в котором изменяется только фаза ф, а амплитуда Л и угловая частота ю неизменны, называют колебанием, модулированным по фазе.

Простейшим амплитудно-модулированным (AM) является колебание, в котором амплитуда модулирована по закону синуса:

/(О =Ло( 1 -(-msinQOsin((ii)/ -(-ф),

где т - глубина модуляции (как правило, m <С 1); 1 - частота модуляции (Q <с; о>).

График АМ-колебания показан на рис. 7.14,а (огибающая дана пунктиром).

Если воспользоваться известным из тригонометрии тождеством sinasinp == cos(a - Э) - cos(a + р),

ТО колебание А{ \ -(-msinS/)sin(co/ -fij)) можно представить в виде суммы трех колебаний:

fit) = osin(a)/ -f ф) -I- -cos((a) - Q)t -f tuAq

+ 1 - -Y-cos[(a) + Q)t H- t)].

Частоту to называют несущей, a частоты (со -Q) и (to --fi) - боковыми. Спектр АМ-колебания изображен на рис. 7.14,6. Действующее значение функции /(/) в соответствии с формулой (7.11)

равно ф11 -h{m/2). 222

пример 74. Разложить на составляющие функцию /(/)=20(1 + -0,6sinl00s»nl0/.

Решение. Боковые частоты о»-й= 99-1 w-f й= 1 О И СР ; тА/2 =6.

Следовательно, /(/) = 20sinl0 + 6cos(99-100 - 6cos(101 • 100-

Амплитуды колебания боковых частот при АМ-колебании зависят от глубины модуляции т, но не зависят от частоты модуляции Q.

Ширина полосы частот, занимаемой АМ-колебанием, не зависит от m и равна (о) -- - (о - Q) = 2й.

Рассмотрим спектры частотно-модулированных (ЧМ) и фазо-модулированных (ФМ) колебаний. Форма колебаний качественно показана на рис. 7.14, в.

Аргумент синусоидально изменяющейся функции /(/) обозначим а(/). Тогда

f(t) = Asm[a(t)], (а)

а(/) можно интерпретировать как угол, на который повернется вращающийся вектор на комплексной плоскости за время /. Угловая частота поворота этого вектора о = da(/) / d/. В том случае, когда (О = (Oq = const,

а() = o)od = (Oq/; f(t) = sinwo.

При частотной модуляции частота о) изменяется и равна (Оо + А(Оф(/). При этом

а() = J[o)o -f Аа)ф(ОМ/ = сод/ -f ii\ц>{t)dt.

При (t) = cosQ

а() - щ1 -\- 7sinQ/, (б)

где 7 = Асо / Q - глубина модуляции.

Таким образом,

f(t) I А - sin((Oo/ -f Ysin/) = sino)/cos(7sinQ/)

-- coso)osin(7SinQ),

sin(7sinQ0 = 2p2«+ i(v)sin(2rt -f- \)Q.t\

cos(7sinQ/) = /0(7) -- 2YJ2n(y)cos2nQt,

Где /(y) - бесселева функция k - порядка от действительного ар-