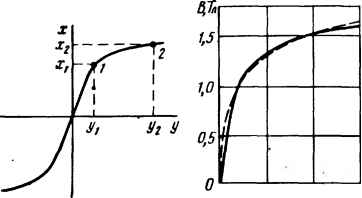woo гоооцф I)

Рис. 15.11

аналитического описания симметричных характеристик по типу рис. 15.11, а будем пользоваться гиперболическим синусом:

у = ashpjc.

(15.1)

В этом выражении аир - числовые коэффициенты; а выражается в тех единицах, что и г/; р - в единицах, обратных единицам х, так что произведение есть величина безразмерная. Для определения неизвестных коэффициентов аир следует на полученной опытным путем зависимости у = f{x) в предполагаемом рабочем диапазоне произвольно выбрать две наиболее характерные точки, через которые должна пройти аналитическая кривая, подставить координаты этих точек в уравнение (15.1) и затем решить систему из двух уравнений с двумя неизвестными.

Пусть координаты этих точек f/j, х и у, Х2(рис. 15.11, а). Тогда

Отношение

у у = ashpx,; у2 = ashpXg.

(15.2)

Трансцендентное уравнение (15.2) служит для определения коэффициента р. Следовательно,

а = f/g/shpjcg. (15.3)

Пример 147. Кривая намагничивания трансформаторной стали Э41 изображена на рис. 15.11, б. Найти коэффициенты аир.

Решение. Выбираем две точки на кривой: j = 200 А/м; В, = 1,1 Тл;

2 = 2400 А/м; fig = 1.532 Тл.

По уравнению (15.2) имеем sh(l,532p)/sh(l,ip) = 12. Задаемся произвольными значениями р и производим подсчеты:

По результатам подсчетов строим кривую shpBg/shpB, = /(Р) и по ней находим Р = 5,75 Тл~. Далее определяем

а = g/shpBg = 2400/sh8,82 = 1200/1690 = 0.71.

Пунктирная кривая на рис. 15.11. б построена по уравнению Н = 0,71sh(5,75B). § 15.14. Понятие о функциях Бесселя. При анализе нелинейных цепей широко используют функции Бесселя, которые являются решением уравнения Бесселя

У = 0.

(15.4)

Функции Бесселя выражают степенными рядами и для них составлены таблицы. Функцию Бесселя от аргумента х обозначают /Дх), где р - порядок функции

Бесселя. Общее выражение для Jp{x) в виде степенного ряда можно записать так:

{х/2)Р {х/2)Р + * {х/2)Р + 1!(р+ 1)! "2!(р +2)! 3!(р + 3)!

/Ы =

+ ....

(15.5)

Таблица 15.1

Для гл. 15 наибольший интерес представляют функции Бесселя от чисто мнимого аргумента (табл. 15.1). Для их получения в общее выражение (15.5) вместо х следует подставить jx, где / = V~l • Обратим внимание на то, что в табл. 15.1 даны функция - jJiiJx) вместо /i(/Jf) и функция jJ[iJx) вместо /з(м)- Сделано это потому,

10 60 50 UO 30 20 W

1 2 3 и 5

Рис. 15.12

что без дополнительного множителя / или - у эти функции, как правило, не используют.

При Jt = О не равна нулю только функция Бесселя нулевого порядка: /q(0) = 1.

Поданным табл. 15.1 на рис. 15.12 построены кривые функции Бесселя. Из таблицы и рис. 15.12 видно, что с ростом х значения функций увеличиваются. Чем выше порядок функции Бесселя, тем меньше ее значение при одном и том же х.

§ 15.15. Разложение гиперболических синуса и косинуса от периодического аргумента в ряды Фурье. Если аргумент х изменяется по периодическому закону, например по закону синуса х = Jtsinco/, где jc - амплитуда колебаний, то по периодическому закону изменяются и функции sh(jtsino)/) и ch(jtsino)/). Так как периодические функции можно представить рядами Фурье, то разложим в ряд Фурье эти функции. С этой целью в (15.5) вместо х подставим jcsinco/. Учтем известные из тригонометрии формулы

sin а = 0,5 - 0,5cos2a;

sin а = ~ 0,25sin3a -- 0,75sina;

sina = 0,375 - 0,5cos2a -- 0,125cos4a,

(15.6)

(15.7) (15.8)

сгруппируем все слагаемые с sino) cos2(0, sin3w и т. д., а также отдельно выделим постоянную составляющую. В результате оказывается, что коэффициентами при тригонометрических функциях являются ряды, которыми изображают функции Бесселя различных порядков от чисто мнимого аргумента jxm- Окончательно получим

sh(xsin(0o=2[- /7/xJ]sinwf--2/73(/xJsin3co--2 5(/xJsin5w-(15.9)

ch(xsinwO = /o(MJ + 2/2(MJcos2w< + 2/4(/xJcos4(o<-h... . (15.10)

Ряд для sh(jcsino)0 состоит только из нечетных гармоник и не имеет постоянной составляющей. Ряд для ch(jtsinwO имеет постоянную составляющую и четные гармоники.

Пример 148. Разложить в ряд Фурье sh(4sino)/) и ch(4sinwO-Решение. Значения функций Бесселя берем из таблицы:

- /7,(/4) = 9,76; з(/4) = 3,34; JjA) = 1,416; - 5(/4) = 0,505; /о(/4) = 11,3; JjA) = - 6,42.