электрических цепей, как, например, эффект усиления мощности. Для исследования свойств резонансных нелинейных цепей метод пригоден в ограниченной степени. Так, им можно приближенно исследовать простейший триггерный эффект(см. § 15.59), но нельзя, например, исследовать резонансные явления на высших гармониках.

§ 15.49. Аналитический метод расчета цепей по первой и одной или нескольким высшим или низшим гармоникам. Основные эт апы расчет а следующие: 1) составляют систему дифференциальных уравнений цепи; 2) аналитически выражают характеристики нелинейных элементов и полученные выражения подставляют в дифференциальные уравнения цепи.

Искомую величину выражают в виде ряда, состоящего из первой и одной или нескольких высших или низших гармоник, например в виде

X = Х,,81П0)/ + Хз,81п(30)/--фз).

Предполагаемое решение подставляют в уравнение системы. В результате этой подстановки оказывается возможным разбить уравнения системы на несколько трансцендентных алгебраических уравнений, составленных относительно амплитуды первой гармоники, амплитуд высших (соответственно низших) гармоник и их фаз.

Число трансцендентных уравнений в общем случае в два раза больше числа учитываемых гармоник, поскольку для каждой из гармоник уравнение разбивается на два уравнения для синусной и косинусной составляющих.

Далее совместно решают систему трансцендентных уравнений. Трудность состоит в том, что каждое из трансцендентных уравнений обычно содержит все неизвестные. Поэтому при решении часто используют метод последовательных приближений. Решение облегчается, если учесть последний абзац § 15.62.

Расчет этим методом, как правило, громоздок. Однако метод позволяет исследовать такие сложные явления в нелинейных цепях, как резонанс на высших, низших и дробных гармониках и т. п.

Рассматриваемый метод в литературе называют также методом гармонического баланса. Частным случаем его является метод первой гармоники (см. § 15.47).

§ 15.50. Расчет цепей с помощью линейных схем замещения. Этот метод применим к расчету нелинейных электрических цепей, на которые воздействуют постоянные и синусоидально изменяющиеся ЭДС, если переменные составляющие токов и напряжений относительно малы, например во много раз меньше соответственно постоянных составляющих токов и напряжений.

Последовательность расчета такова:

1) определяют положение рабочей точки на характеристике нелинейного элемента по постоянному току. В окрестности этой точки будет перемещаться изображающая точка под воздействием малой переменной ЭДС;

2) через рабочую точку по постоянному току проводят касательную к характеристике нелинейного элемента и производят замену учае1кл сю характеристики отрезком касательной;

3) составляют линейную схему замещения для расчета переменной составляющей. Вид схемы зависит от характера нелинейного элемента, а ее параметры - от тангенса угла, составленного касательной к характеристике и одной из осей координат.

ЭВМ применяют для: а)табулирования решений систем трансцендентных уравнений и систем алгебраических уравнений высоких степеней; б) табулирования решений, выраженных в виде медленно сходящихся рядов; в) интегрирования систем линейных дифференциальных уравнений, к которым сводятся нелинейные дифференциальные уравнения при кусочно-линейной аппроксимации характеристик нелинейных элементов; г) численного интегрирования нелинейных дифференциальных уравнений, в которых ВАХ нелинейных элементов представлены аналитически, а также в некоторых других случаях.

Рис.1533

§ 15.51. Расчет цепей, содержащих индуктивные катушки, сердечники которых имеют почти прямоугольную кривую намагничивания. Кривые намагничивания некоторых высококачественных магнитомягких материалов, например 65НП, 68НМП и др., близки по форме к прямоугольной: на участке О - а (рис. 15.33, а) кривая почти совпадает с осью ординат, а на участке а - Ь расположена почти параллельно оси абсцисс.

На рис. 15.33, а пунктиром показана предельная петля гистерезиса. Коэрцитивная сила для таких материалов очень мала и составляет 1 - 10 А/м.

Расчет электрических цепей переменного тока, содержащих индуктивные катушки, сердечники которых выполнены из упомянутых магнитных материалов, обычно производят с помощью метода кусочно-линейной аппроксимации (см. § 15.46). Для облегчения расчета кривую намагничивания заменяют идеально прямоугольной (рис. 15.33, б). Участки 4 - / и 2 - 3 параллельны оси абсцисс, а участок / - 2 совпадает с осью ординат.

Если изображающая точка перемещается по участку / - 2, то изменяется только индукция в сердечнике при напряженности поля в сердечнике, почти равной нулю. При движении изображающей точки по участкам 4 - / и 2 - 3 меняется только напряженность поля , а индукция в сердечнике остается неизменной.

Пример 155. Схема (рис. 15.33, в) состоит из источника синусоидальной ЭДС u=e=£sino)/, индуктивной катушки с заданной зависимостью потокосцепления гр

от тока i и резистора сопротивлением R. Вывести формулу для определения ф и / и построить графики изменения ф и t во времени в установившемся режиме.

Решение. Так как потокосцепление ф равно произведению индукции в сердечнике В на площадь поперечного сечения сердечника и на число витков обмотки: ф = BSm, а по закону полного тока, ток i == Hl/w, т. е. пропорционален напряжеино-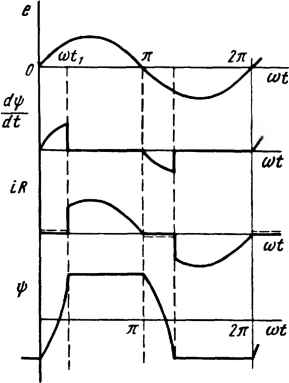

Рис. 15.34

Рис. 15.35

сти магнитного поля в сердечнике, то зависимость потокосцепления ф от тока / (рис 15.33, г) качественно такая же, как и зависимость В=/( )(рис. 15.33, б). Имеем

dxi) „ (15.53)

В интервале времени от й)/=0 до о)/ = о)< (назовем его первым) ток /=0, все напряжение приходится на индуктивную катушку dij)/d/=£,sin(«) и потокосцепление ф изменяется от -до (изображающая точка на рис. 15.33, б перемещается от / к 2).

В этом интервале = £sino)<d; следовательно.

"т

coso)-bC,

(15.54)

где С - постоянная интегрирования.

Во втором интервале времени от о) = о), до со = л потокосцепление ф остается

постоянным и равным ф,; d/d = 0; из уравнения (15.33) получим

(15.55)

Ri = £,sinfa>/, или / = sinto/.

Таким образом, во втором интервале времени ток / изменяется по закону синуса, потокосцепление ф постоянно и равно ф. При этом изображающая точка перемещается по участку 2 - 5 (рис. 15.33, б).

Найдем постоянную интегрирования С и значение to/,. Для определения С запишем уравнение (15.54) при (at - 0. Для этого момента времени »!)=- поэтому - = / W + С. Отсюда С = - ф, -f £, / О).

Для нахождения o)j воспользуемся также уравнением (15.54), учтя, что при си/ = (д/ ф = ф. Получим

= - -COSC0/, - +