
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) ( 59 ) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (59) 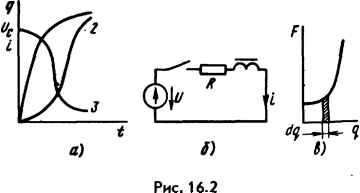 Разделим переменные: At=R Пя)=- или dt=RF{g)dq, (16.1а) (16.2) и-им Для построения кривой Р{д)(рис. 16.1, б)используем КВХ. Левую часть уравнения (16.1а) проинтегрируем по / от О до текущего значения /, а правую по - от =0 до текущего значения д. В результате получим t==RF{q)dq. (16.3) Графически подынтегральное выражение F()d представляет собой заштрихованную площадку (рис. 16.1, в). Кривая / на рис. 16.2, а качественно представляет собой зависимость от /. С помощью кривой q=f(t) и КВХ нелинейного конденсатора строят зависимость ut) (кривая 2). Ток в цепи для произвольного момента времени определяется по формуле i={U-Uf2)/R (кривая 3). § 16.3. Расчет методом интегрируемой нелинейной аппроксимации. Данный метод основан на аппроксимации характеристики нелинейного элемента такой нелинейной функцией, которая, во-первых, достаточно точно отображает его характеристику в предполагаемом интервале перемещения изображающей точки по ней и, во-вторых (и это главное), дает возможность точно проинтегрировать уравнение в известных функциях. Ценность метода заключается в том, что в результате интегрирования получают зависимость исследуемой величины от времени и всех параметров схемы. Метод применим к дифференциальным уравнениям первого порядка, а также к уравнениям, сводящимся к уравнениям первого порядка путем замены переменных. Пример 161. Определить закон нарастания во времени тока при замыкании ключа в схеме (рис. 16.2, б). Зависимость тока от потокосцепления ф выражена формулой i=k\p . В схеме нулевые начальные условия. P e Ш e H и e. Из уравнения цепи -r~-\-Ri=U следует, что dt=--- Вынесем ut и - t\l из знаменателя множитель R и заменим i на Лф- где Iy=U/R. Обозначим I =а и заменим kip на dl)? на dj/F. В результате получим 1 di 1 1 Rk а2-ф{ а2-ф{ 2а I fl-ф? а+ф? 2/0.750,25 0,51n±-farctg77; (16.4) С помощью (16.4) можно определить время, которое необходимо, чтобы отношение i y достигло заданного значения. § 16.4. Расчет методом кусочно-линейной аппроксимации. При расчете этим методом осуществляется замена характеристики нелинейного элемента отрезками прямых линий, что позволяет перейти от нелинейного дифференциального уравнения к нескольким линейным уравнениям, отличающимся друг от друга лишьзначени-ями коэффициента. Каждое из линейных уравнений справедливо для того интервала времени, в течение которого рабочая точка перемещается по соответствующему линеаризованному участку. Метод применим к цепям, содержащим источники постоянной и (или) синусоидальной ЭДС, а также к цепям первого и более высоких порядков. Для сложных нелинейных цепей с источником (источниками) синусоидальной ЭДС основная трудность расчета данным методом заключается в определении постоянных интегрирования, исходя из законов коммутации и времени работы на каждом линейном участке. В сложных цепях неизвестные находят обычно из трансцендентных уравнений, часто применяют ЭВМ. Впервые идея этого метода была высказана русским физиком Н. Д. Папалекси в 1912 г. Рассмотрим основные этапы расчета на простейшем примере. пример 162. Конденсатор емкостью С заряжается через HP от источника постоянного напряжения U (рис. 16.3, а). Определить закон изменения тока в цепи при зарядке. 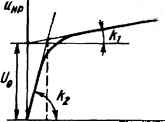 Решение. ВАХ HP заменим двумя отрезками прямых линий (рис. 16.3, б). Пусть на участке от /=0 до /=tj «„p=2, " "нр - напряжение на нелинейном резисторе; fcg - коэффициент. На участке />/, M„p=f/oH~i- Размерность коэффициентов Л, и соответствует размерности сопротивления. В уравнение цепи Ис+"нр= вместо подставим - idt, заменим и для первого участка на f/Q+fe,/, а для второго - на g. При зарядке конденсатора ток постепенно уменьшается от максимального значения до нуля. Поэтому изображающая точка перемещается сначала по первому участку, а затем по второму. Для первого участка - id+f/Q-f ,i=f/; для второго - idt-\-li2i=U. Для первого участка i=iJp-\-i=0-\-Ae~i. Постоянную интегрирования А1 найдем из начального условия: t=0, м=0. Поэтому UQ-\-kyi{0)=U и i{0)=Ay={U-f/p)/!- Следовательно, при работе на первом участке Пусть при =1 ток Подставим в (16.5) i, вместо / и вместо t и решим полученное уравнение относительно /,: (16.6) , причем 2=tV При работе на втором участке i=2e § 16.5. Расчет переходных процессов в нелинейных цепях методом переменных состояния на ЭВМ. Рассмотрим методику расчета, используя понятия дифференциальной индуктивности индуктивной катушки L{i)=~ и дифференциальной емкости Сд„ф("с)=" нелинейного конденсатора. Если вебер-амперная характеристика индуктивной катушки /=ashpi3, то диф(0= рУ .у 2- Если кулон-вольтная характеристи- ка конденсатора U(-ashbq, то Сдф(м) 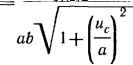 Пример 163. Составить систему уравнений по методу переменных состояния для схемы (рис. 16.4) при нулевых начальных условиях и указанных на рисунке положительных направлениях отсчетов токов и напряжений. Решение. Из уравнения i=i2+3 следует 1=17+ R dur dt Из уравнения Ф г. dф dt г. , / ч ~Uc=E имеем --+«0= "-"и L„(f)- (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) ( 59 ) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) |
|
|