4, ;

Рис. 16.11

Вид фазовой траектории зависит от конфигурации схемы, характера нелинейности и соотношения между параметрами.

Если процесс в цепи является периодическим, то через интервалы времени, равные периоду процесса, соответствующие друг другу значения хиу повторяются и фазовая траектория в этом случае является замкнутой кривой. Замкнутую фазовую траекторию называют предельным циклом.

Если интегральные кривые и снаружи и изнутри навиваются на предельный цикл, то его называют устойчивым, если удаляются от него - неустойчивым. Если же процесс непериодический, то фазовая траектория представляет собой незамкнутую кривую.

Фазовую траекторию можно наблюдать на экране электронно-лучевого осциллографа. С этой целью на одну пару отклоняющих пластин его подают исследуемую величину X, а на другую пару - производную от х.

§ 16.16. Изображение простейших процессов на фазовой плоскости. Рассмотрим Несколько простейших примеров.

j< Требуется изобразить на ФП переходный процесс в схеме на рис. 16.11, а, вызываемый при нулевых начальных условиях замыканием ключа. Обозначим: / - ток в цепи, - напряжение на конденсаторе. В уравнение цепи/?г -\- Uq = £ вместо

/ подставим С-

Положим Ur = X, duf~./dt = у, тогда у = {Е - x)/{RC).

Последнее уравнение описывает прямую аЬ (рис. 16.11, б), которая является фазовой траекторией рассматриваемого процесса (точка b - точка равновесия). , Рассмотрим изображение на ФП синусоидального колебания / = lsiniot (рис.

16Л1,в).

dx I

Обозначим / = X, тогда у = - - co/cosco/, т. е. л; = /sinco/,

у = (0/СО5(0Л

Разделив первое уравнение на 1, второе - на и/, возведя в квадрат получен-

Рис. 16.12

ные выражения и сложив их, получим уравнение эллипса

= 1.

Следовательно, изображением синусоидального процесса (фазовой траекторией) на ФП является эллипс (рис. 16.11, г).

Направление движения изображающей точки показано стрелкой. В верхней йх

полуплоскости у = следовательно, изображающая точка движется в сторону

йх

увеличения координаты х. В нижней полуплоскости "О» поэтому изображающая

точка движется в сторону уменьшения координаты х. В целом перемещение изображающей точки на ФП происходит всегда по часовой стрелке.

§ 16.17. Изоклины. Особые точки. Построение фазовых траекторий. Тангенс угла наклона, образованного касательной к интегральной кривой в некоторой точке ФП и осью абсцисс, определяет значение йу/йхв этой точке. Совокупность т очек ФП, для которых diz/djc = const, называют изоАслиной. На ФП можно провести множество изоклин, каждой из которых соответствует свое значение.

Для всех точек ФП, отражающей процессы в цепи второго порядка (кроме особых точек), dy/dx имеет вполне определенное значение. В особых точках (ОТ) dy/dx = О/О, т. е. не определено. Через эти точки может быть проведено множество изоклин с различными значениями dy/dx.

ОТ классифицируют по виду интегральных кривых, окружающих эти точки.

Если ОТ окружена эллипсами (рис. 16.11, д), то ее называют ОТ типа центр; она соответствует двум мнимым корням характеристического уравнения.

Если ОТ окружена свертывающейся спиралью, то ее называют устойчивым фокусом (рис. 16.11, е); ей соответствуют комплексно-сопряженные корни с отрицательной действительной частью.

Если ОТ окружена раскручивающейся спиралью, то ее называют неустойчивым фокусом (рис. 16.11, ж); ей соответствуют комплексно-сопряженные корни с положительной действительной частью.

Если корни отрицательные и действительные, то ОТ называют устойчивым узлом (рис. 16.11, з). при положительных действительных корнях получают ОТ типа неустойчивого (рис. 16.11, и). Когда один корень положителен, а другой отрицателен, имеем ОТ типа седла (рис. 16.11, ас).

Рассмотрим переходный процесс в схеме на рис. 16.12, а, вызываемый замыканием ключа при нулевых начальных условиях: £ = 1 В; /? = 1 Ом; L = 1 Гн; С = 1 Ф-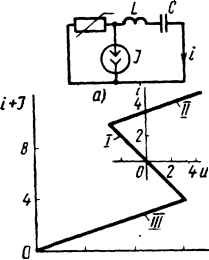

/7 а=2 J О.у

и 8 12 и*и щ S)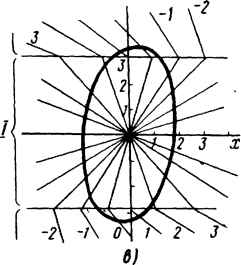

Рис. 16.13

Построим семейство изоклин для напряжения на конденсаторе ис. Определим положение и тип ОТ. Построим фазовую траекторию переходного процесса.

В уравнении цепи LC

duc\

duc due

-\- RC-jY -\- uc = E заменим uc на x, -- на у.

dt dt

d dy dx dy , n с 1 n

y на ~Г"77~УТ~ учтем, что L = k = C = c = I. Решим уравнение

dx dt

y-- у X = 1 относительно у и dy/dx: ил

1 -f dy/dx dy \ -x - у

Из уравнения (б) следует, что координаты особой точки у = 0, х = 1. Последовательно придавая dy/dx значения О, 1,2,- 1, -2, оо, строим семейство изоклин (рис. 16.12, б). Все изоклины проходят через ОТ и представляют собой прямые линии (цепь линейна). Масштабы по осям хну приняты одинаковыми. Черточки на каждой изоклине характеризуют значение d/dx для нее.

duc\

Так как х(0) = ыс(0) = О и у{0) =

= О, то к началу процесса изображаю-

щая точка находится в начале координат. В установившемся режиме х = 1 и = 0.

Для построения интегральной кривой из исходной точки х = у = О проводим два луча до пересечения с изоклиной dy/dx = 1 в точках тип: Первый луч соответствует значению dy/dx = оо той изоклины, с которой начинается движение, второй - значению- = 1 следующей изоклины, на которую точка перейдет. Делим расстояние

тп пополам и проводим через исходную и полученную точки плавную кривую - кусочек фазовой траектории. Продолжаем аналитический процесс далее и строим всю фазовую траекторию в виде свертывающейся спирали.

от в примере является устойчивым фокусом. Время в явном виде на фазовой плоскости не отражено.

Временные зависимости х = /(/) по фазовой траектории У ~ получа-