емкость, называемая часто «паразитной», и /?доб> О - некоторое добавочное активное сопротивление. Параметры и R, а также Сп и /?доб зависят от физических процессов в HP и изменяются при переходе из одной точки на падающем участке ВАХ в другую.

§ 17.4. Исследование устойчивости автоколебаний и вынужденных колебаний по первой гармонике. Исходными при исследовании устойчивости автоколебаний и вынужденных колебаний обычно являются уравнения, получаемые по методу медленно меняющихся амплитуд (см. § 16.6). Однако в тех случаях, когда напряжение на каком-либо элементе (ток в исследуемой цепи) резко отличается по форме от синусоиды, например имеет пикообразную форму, исследование устойчивости целесообразно проводить по средним за полпериода значениям величин.

Если через awb обозначить медленно меняющиеся амплитуды синусной и косинусной составляющих исследуемого колебания, то из исходных уравнений системы можно получить два уравнения для медленно меняющихся амплитуд:

Ла/Л1 = А(а,Ь1 /Г; •. . (17.1)

db/dt = В(а, Ь).

(17.2)

Здесь Л и В являются функциями амплитуд а и Ь, функциями параметров схемы, угловой частоты колебаний со и амплитуды вынуждающей силы. Обозначим значения а и b в установившемся режиме (когда амплитуды не изменяются во времени) через и Ь. Для определения и Ь в (17.1) и (17.2) следует положить da/dt = О к db/dt = О и решить систему уравнений:

• • Л(ао,6о) = 0; . (17.3)

В{а, 6о) = 0.

(17.4)

Пусть в результате возмущения амплитуды колебания получили малые приращения Аа и А6 и стали равными: а = «о + Аа и Ь = Ь-\- Л6.

Подставим эти значения а и b в (17.1) и (17.2), разложим A(aQ + Аа, Ь -\- АЬ) и B{aQ + Аа, 6о + АЬ) в ряд Тейлора по малым приращениям Аа и АЬ, в силу малости приращений ограничимся слагаемыми ряда с первыми степенями Аа и АЬ. В результате получим:

Л («о + Аа, 0 + А6) = Л(ао, Ь) + АаЛ, + А65„ (17.5) В{а + Аа, 6о + АЬ) = В(а, Ь) + АаА + АЬВ. (17.6)

Для сокращения записи обозначено:

дА{а, Ь)

дА{а, Ь)

(17.7)

дВ{а, b)

; Br, =

дВ{а, b)

(17.8)

Индекс у свидетельствует о том, что в частные производные должны быть подставлены значения а и b установившегося режима, т. е. 0 и

Коэффициенты Л,, Ag. 2 являются функциями Gq и bQ, но не являются функциями приращений Да и Д6. Подставим правые части (17.5) и (17.6) в(17.1) и (17.2), учтя при этом (17.3) и (17.4), а также то, что

. с1(ао + Аа) dAa d(&o + А&) dA& ; .• . .

и -

dt dt di dt

в результате получим два уравнения: " .

da/dt = Aa-\-ВАЬ\

dM/dt = a2a -f Bb.

Алгебраизируем их: "

рДа = Д,Да + ,Д6;

• - . /V Pb = ЛзДа + Bb. Составим характеристическое уравнение

q = Ab2-Ba2.

(17.9) (17.10)

(17.9а) (17.106)

(17.11)

(17.12) (17.13)

В соответствии с критерием Гурвица для затухания приращений Да и Д6 необходимо, чтобы

т>0, >0.

(17.14)

В автоколебательных системах периодические вынуждающие силы, как правило, отсутствуют, поэтому можно принять Ь = 0,т. е. взять колебание в виде a(/)sinco (см. пример 164). В этом случае вместо двух уравнений (17.9) и (17.10) будет одно уравнение

dAa/d/ = 4iAa, . (17.15)

dЛ(a)

(17.16)

а = Ur

Для устойчивости автоколебаний в этом случае необходимо выполнение условия Л,<: 0.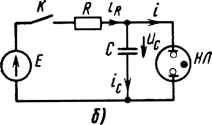

Рис. 17.3

Пример на исследование устойчивости автоколебаний по формуле (17.15) см. в § 17.6.

§ 17.5. Исследование устойчивости состояния равновесия в генераторе релаксационных колебаний. Релаксационные колебания представляют собой автоколебания, при определенных условиях возникающие в нелинейных электрических цепях с одним накопителем энергии, например в цепи с одним конденсатором (без индуктивного элемента) или одним индуктивным элементом (без конденсатора).

На рис. 17.3, а изображена принципиальная схема генератора релаксационных колебаний. Она состоит из источника постоянной ЭДС £, линейного резистора сопротивлением R, конденсатора емкостью С и параллельно соединенного с ним нелинейного резистора, имеющего ВАХ S-образной формы.

В качестве HP с такой ВАХ могут быть взяты неоновая лампа или тиратрон. На рис. 17.3, б дана схема генератора с неоновой лампой. Кривая / (рис. 17.3, в) представляет собой ВАХ неоновой лампы, прямая 2 - ВАХ R.

Если бы не было релаксационных колебаний, то режим работы определился бы точкой т пересечения кривой / и прямой 2. Для этой точки сумма падений напряжений на HP и R ь соответствии со вторым законом Кирхгофа равна ЭДС Е: iR -f Uhr = £.

Точку m будем называть точкой равновесия. Она определяет режим работы схемы при прохождении по/? и неоновой лампе постоянного тока.

Убедимся в том, что режим работы, определяемой точкой т, является неустойчивым: достаточно ничтожно малого отклонения от состояния равновесия, чтобы изображающая точка «ущла» из точки w и не возвратилась в нее. В схеме возникнут релаксационные колебания.

Для того чтобы убедиться в неустойчивости состояния равновесия, составим линейную схему замещения релаксационного генератора.

Так как HP имеет S-образную ВАХ, то в схеме для исследования устойчивости оно имитировано (в соответствии с§ 17.3) дифференциальным сопротивлением /?диф и последовательно с ним включенной малой паразитной индуктивностью А,, зашун-тированной резистором сопротивлением /?доб-

Исследование устойчивости вынужденных колебаний на высших гармониках и субгармониках, процессов в цепях с переменными во времени параметрами, а также исследование устойчивости процессов автомодуляции даны, например, в [20].