§ 3.3. Спектр пространственных частот изображения

При определении спектра пространственных частот будем исходить из условия, что передаваемое изображение неподвижно. Тогда распределение освещенности в изображении Е{х, у) можно разложить в ряд Фурье. Вдоль прямой, параллельной оси х и проходящей через точку с координатами х и у (рис. 3.6), распределение освещенности может быть представлено в виде ряда [10

Е(х, У) = Е„

{у) cos

(3.9)

где т=1/кт - число периодов, укладывающихся на ширине изображения /, Km - период изменения яркости; Ет(у)-амплитуда; фт - начальная фаза т-го компонента.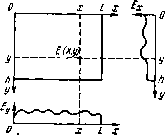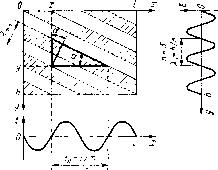

Рис. 3.6. Распределение освещенности по осям x к у

Рис. 3.7. Компоненты пространственных частот изображения

Поскольку амплитуда т-го компонента зависит от координаты у, она также может быть представлена в виде ряда

cos + (3.10)

где Хп - период изменения яркости; n-h/Xn - число периодов, укладывающихся на высоте изображения Л; Е"тп - амплитуда т-го компонента по ширине и п-го компонента по высоте изображения; ф„ -начальная фаза.

Подставив соотношение (ЗЛО) в (3.9), представим распределение освешенности в виде двойного ряда

00 оо

(2лт

о л-0

2ят

\ I 2лп

(3.11)

4" COS где £mn = £"mn/2.

Так как при фиксированном т слагаемые, содержащие п в аргументе первой косинусоидальной зависимости ряда (3.11), изменяются от О до +00, а в аргументе второй - от О до -оо, то оба компонента можно объединить, изменив соответственно пределы

суммирования по П и обозначая фт,+п = фт + фп и <рт,-п = фт-фп.

Тогда можно записать

или в комплексной форме

(3.12)

(3.13)

где Етп = Етп/2.

в качестве примера на рис. 3.7 показано распределение косинусоидальной пространственной волны с числом периодов изменения яркости т=2 по ширине изображения и л = 3 по высоте изображения, при этом отрицательные полуволны отмечены штрихов- кой. Видно, что Ят И Я„ есть проекции периода пространственной волны Хтп на оси координат. Из подобия треугольников следует

cos =Х„„/Х„=Х„ / Yll -f Х,

откуда период пространственной волны

/ (/и )2 + (n/h)2

И угол наклона

а„„=arctg (Х„/Х„)=arctg (hmjln).

Таким образом, любое изображение может быть представлено в виде суммы бесконечного числа пространственных косинусоидальных волн с 0т=1/Хт + оо и -ооп=Л/Хп--оо- Содержанием передаваемого изображения определяются амплитуды Етп и начальные фазы <ртп компонентов тп ряда.

§ 3.4. Пространственная фильтрация изображения в телевизионной системе

В сигнал одновременно преобразуется световой поток, усредняемый в пределах площади апертуры Д5. Характеристики преобразования зависят от распределения прозрачности р{х, у) разлагающего элемента.

Если освещенность в передаваемом оптическом изображении Е{х, у) зависит от координат хну, которыми характеризуется положение центра апертуры О (рис. 3.8), то иа элементарном участке 5, выделяемом в пределах площади Д5, освещенность Eds(x+x, у+у) зависит еще и от координат х и у участка dS относительно центра О.

Составляющая светового потока d0=Eds{x+x, y+y)dxdy, падающего иа участок dS=dxdy, и распределение прозрачности р(х, у) определяют составляющую d0=p(x, y)d0, прошедшую через элементарный участок dS.

Б линейной системе приращения фототока пропорциональны приращениям светового потока. Интегрирование составляющих фототока di=Bd0 от участков dS с интегральной чувствительностью е фотослоя по всей площади AS позволяет определить ток сигнала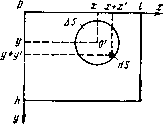

Рис. 3.8. Координаты участков изображения Д5 и dS

Eas(x-\-x\y-\-y)9 (х, у) dxdy.

(3.14)

В частном случае, при неизменной освещенности изображения (£o=const), в соответствии с (3.14) достигается установившееся значение сигнала

<о=е£„ ГГ р(>:. y)dxdy = E,P, (3.15)

определяемое интегральной прозрачностью всей апертуры

Po==jp(, (3.16)

Переходные процессы. При передаче резкой границы с изменением освещенности от нуля до £о (рис. 3.9), совмещенной с началом координаты х, текущее значение сигнала

1(х)=гЕ, If р(х\ y)dxdy = E,P(x) (3.17)