и одновременно вынесем из-под знака суммирования значение средней освещенности £о- Здесь Мт=Ет/Ео - глубина модуляции т-го компонента с периодом изменения яркости Хт = 1/т и амплитудой Ет-

В апертурном сечении dx (рис. 3.11), удаленном на расстояние х от среднего сечения, положение которого, в свою очередь, определяется координатой х, освещен-яость изображения

£(х+х)=Ео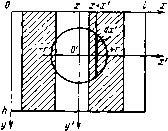

Составляющая светового потока d0=E{x-\-x)dx, падающего на сече- Рис 3.11. К определению поло-ние dx, и прозрачность сечеиия (3.20) «е""" апертуриого сечения определяют составляющую dФ- =R(x)d0, прошедшую через это сечение.

В предположении линейности системы, суммируя составляющие фототока di=edФ по всей площади апертуры радиусом г, найдем текущее значение сигнала

Rix)dx. (3.27)

Вынося за скобки множитель I-bEq Fi{x)dx= гЕР-~

среднюю составляющую сигнала, меняя порядок суммирования и интегрирования во втором слагаемом и группируя отдельно сомножители, зависящие от переменной х, по которой ведется интегрирование, представим соотношение (3.27) в виде

f 2 77 J () ехр (у dxM„ ехр

/ .2л

1+2»Аехр(у

отличающемся от (3.26) тем, что глубина модуляции т-х компонентов пространственных частот изменяется в соответствии с сомножителем Ьт-

Соотношение

». = -J R(x)exp[-jjxdx, (3.28)

определяюшее апертурно-частотную характеристику сканируюшего устройства, отличается от т противоположным направлением оси х, по которой ведется интегрирование, поскольку в используемой системе координат для любой фиксированной точки изображения значение х + х-с остается неизменным и, следовательно, в процессе развертки с ростом х значение х = с-х уменьшается.

10,50

-0,25

Рис. 3.12. Апертурно-частотиые характеристики

Проиллюстрируем апертурно-частотные характеристики иа ряде примеров.

При равномерном распределении световой чувствительности в пределах элемента размером dXd имеем апертурно-частотную характеристику

. 2я ..,\ ,... б1п(я/Х„) 29

-а 12

x\dx=

(кривая / на рис. 3.12). В случае гауссова закона распределения плотности электронов по сечению пучка с условным диаметром с?е=2ле в передающей (приемной) трубке имеем

dx = exp

(3.30)

(кривая 2 на рис. 3.12). Кривая / имеет точки пересечения с осью абсцисс при целочисленных значениях отношения d/Xm, кривая 2, изменяющаяся по гауссову закону, оси абсцисс не пересекает.

Апертурно-частотная характеристика ТВС с неограниченной полосой пропускания в канале связи и одинаковыми законами рас-

пределения прозрачности в апертурах на передающей и приемной стороне определяется квадратом выражения (3.28). В частных случаях рассмотренных распределений эта характеристика определяется квадратами выражений (3.29) и (3.30) (кривые 3 и 4 на рис. 3.12).

Конечные размеры апертур приводят к низкочастотной пространственной фильтрации изображений, ограничению глубины модуляции и числа компонентов пространственных частот, а следовательно, и к снижению четкости изображений. Количественно разрешающая способность ТВС оценивается числом полупериодов

2т=2- пространственной частоты, воспроизводимой с глу-d \т

биной модуляции, определяемой отсчетным уровнем До. Продольная разрешающая способность ТВС ограничивается также полосой частот в канале связи (кривая 5 на рис. 3.12), а поперечная - дискретизацией изображения строчным растром. При передаче движущихся в поперечном направлении изображений, как и при поперечном скольжении строк, растет число отсчетов, уменьшается влияние строчного растра и поперечная разрешающая способность приближается к значению, определяемому апертурной фильтрацией.

С прямоугольной частотной характеристикой канала связи и граничной частотой (3.8), определяемой условием передачи пространственной частоты Fx-1/Х с периодом изменения яркости Х=2б, хорошо согласуется распределение прозрачности в апертуре

(см. рис. 3.3, е). Реальные распределения отличаются от теоретических, что ослабляет глубину модуляции сигнала в полосе прозрачности канала и приводит к появлению спектра частот за пределами полосы пропускания канала.

Для обеспечения заданной разрешающей способности ms ТВС в целом разрешающие способности mi и тц ее передающего и приемного звеньев должны быть больше ms. Например, в случае гауссова закона (3.2) распределения прозрачности в апертурах и при неограниченной полосе пропускания в канале связи зависимость между разрешающими способностями определяется соотношением

1 й=1 й+1 га?„

откуда при mi=mii=m имеем m=]/ms-

Апертурно-растровая фильтрация. Изображение в ТВС подвергается не только апертурной, но и растровой пространственной фильтрации. В случае одномерной (строчной) дискретизации растровая фильтрация отражается на характеристиках поперечного разложения изображения. При двумерной (точечной) дискретизации растровая фильтрация влияет не только на поперечные, но и на продольные характеристики изображения.