только колбочковый аппарат. Таким образом, световой динамический диапазон глаза составляет около 10 Такой широкий динамический диапазон обусловлен прежде всего сложными фотохимическими Процессами разложевшя Зрительного пурпура и в меньшей степени явлениями, связатг-ными с автоматическим регулированием воздействующего на сетчатку светового потока в результате изменения диаметра зрачка (диафрагмирования).

Диапазон длин волн, в котором глаз реагирует на электромагнитное излучение, составляет от 380 до 760 нм. В этом диапазоне длин волн атмосфера, окружающая [ошу планету, обладает наибольшей прозрачностью, что р,, 2.3 Кривая относительной

свидетельствует о том, что свойства видности глаза

глаза формировались в результате многовековой эволюции живых организмов.

В пределах указанного диапазона чувстВг1тельность глаза неодинакова. Кривая, определяЮЕная чувствительность глаза к различным длИЕ!ам волн, называется кривой относительной видности (кривая / на рис, 2.3), Следует заметить, что при существенном уменьшении яркости кривая относительной аидности изменяется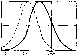

(кривая 2 на рис. 2.3). Прн малых яркостях кривая смещается в сторону более коротковолнового излучения, что приводит к увеличению чуастяительност!) глаза к синим лучам и резкому ее снижению к красЕ1Ым -яв-1еяце Пуркипье.

Указанная характеристика является исходной при согласовании характеристик устройств ТВС с .характеристиками зрения человека.

Феноменологическая модель темвювой и световой адаптации разработана советским ученым П. П, Лазаревым; она дает представление о механизмах адаптации и пряноднг к возможности количе-

ственного описа1{ия [[зйлюдаемых явлений. Теория алаптации описывает изменевше чувствительности глаза при переходе от стационарного освещенного состояния к большей или меньшей освещен-лости. Графически эти зависимости дли разных исходных осаещек-ностей приведены иа рис. 2.4. Как подтверждают измерения, время темноаон адаптации составляет десятки мие!ут (30-50 мин), а световой - единицы минут (8-10 мин) Явления темновой и световой адаптации должны учитываться при проектировании систем и наблюдении изображений человеком в условиях нестационарного освещения (изображение флюоресцирующего экрана или экрана электронно-оптического преобразователя в рентгенодиагностике, телевизионные изображения прн быстрых изменениях внешнего освещения и др.).

§ 2.3. Восприятие яркости к число различимых гразаций

Если ка глаз воздействует изображение с яркостью участков L. то, как показывают эксперименты, наблюдатель реагирует не на абсолютное иэменевше яркости Д1, а на ее относительное значение AL/L. Минимальное относительное изменение яркости M/L. воспринимаемое наблюдателем, называется относительным разностным порогом раздражения. Разностный порог в определенных пределах изменения Интенсивности остается постоянной величиной. Таким образом, минимальное заметное прирашение ошущения в установленных пределах инте[!с1шностей пропорционально относительному разностному порогу:

Ek\L;L, (2.1)

где k - коэффициент пропорциональности.

Если сделать допущение о том. что эта заковюмерность, установ-ленння экспериментально для конечных приращениЛ интелсивно-стей, справедлива для бесконечно малых значений, то соотношение (2,1) приведет к выражению d=.kdL/L. Интегрируя это уравнение, нетрудно определить

AS = ArlnZ,-b«. (2.2)

Постоянную интегрирования Z> определим из условия Н = 0 при i = = /-!,, т. е. £1=-ftlnln. Тогда соотношение (2,2) примет вид

ЛЕ=Л1г,(/. L.), (2.3)

Соотношение (2.3), называемое законом Вебера -Фехнера. устанавливает, что ощущение 3 пропочиоигльно логариф>а>1 яркости L-Экспериментальные исследования (рис, 2.5) позволили установить, что этот закон справедлив в диапазоне яркостей от десятых долей до кд/м= (а на рис. 2.5). где AL/L = An = const. Заштрихована область относительных значений яркости, соответствующая различ-1[ым длинам волн воздействующего излучения.

практика показывает, что чаще всего в реальных условиях работы глаза можно считать справедливым соотношение (2.3).

Определим для этого случая (область а на рнс. 2.5) число регистрируемых глазом градаций яркости на примере ступенчатого клина яркостей с пороговым значением различия но яркости на каждой ступени. Первая градация такого клина отличима от фона,

Рнс 2.5. Результаты экспериментальных нсследованнй относительных пороговых значений яркости

Рнс. 2 6. Зависимость различимых градаций от раста изображения

если ее яркость Lj превышает яркость фонового раздражения Lф на величину £.фДп:

А = -ф + Мп = ф(1+Лп)-Вторая градация отличима от первой, если

L, = L,-j-L, Д„ = L, (1-Ь Д„) =/.ф (1-Ь Д„)2. Аналогично для третьей градации L3=L( 1 +Дп) .

(2 4)

СледовательЕю. для Л-й градации

Из соотношения (2.4) нетрудно определить число разл\ градаций Л, если известен относительный разностгшй порог Дп: 1п (Ln/Lф) Aln (1 --Дп), Учитывая, что L„/Lj,==/( - контраст изображения ступенчатого клина, имеем

n = i\i\k) 1п(1--ДД (2.5)

Таким образом, число различимых градаций Л определяется не только относительным разностным порогом раздражения Дп. но и контрастом к наблюдаемого изображения. Эта зависимость для различных Д„ приведена на рнс 2.6. Расчет показывает, что при Д=100 (черный бархат с коэффициентом отражеЕ1МЯ 0,009 на снегу с коэффициентом отражения 0,9) и A,, = 0,02 ч[есло различимых градаций ,V = 232.

Рассмотренные закономерности лежат в основе выбора динамического диапазона яркостей и контрастности изображения на экра-