ресов ячеек памяти и. следовательно, наиболее простое отыскание любого элемента изображения.

Линейные цифровые фильтры. Цифровым фильтром (ЦФ) называют устройство, преобразующее последовательность отсчета» входного сигнала хо, д-,, х. .... а последовательность отсчетов выходного Сигнала уо. у\, У2, Если в ТВС был нолучен цифроной сигнал, то его последующую обработку стараются провести цифровыми методами, используя при этом широкие возможности цифровой техники и исключая характерное для аналогового тракта накопление искажений.

Рассмотрим особенности структуры линейных ЦФ на некоторых несложных примерах.

Фильтр считают линейным, если справедлив принцип суперпозиции и сумма любого числа входных сигналов преобразуется в сумму откликов на отдельные слагаемые. Реакцию ЦФ на едштч-нын импульс (100 ) называют импульсной характеристикой ЦФ. Фил[,тр называют стационарным, если импульсная характеристика не зависит от времени. Г1ри смещении единичного импульса на очре.1елек11ое число интервалов дискретизации на такое же число интервалов дискретизации смещается и отклик стационарного фильтра.

Из условий линейности и стационарности следует, что каждый выходной отсчет формируется в результате взвешенного суммирования всех предыдущих отсчетов входного сигнала и весовыми коэффициентами являются отсчеты импульсной переходной функции

y=Xak;\-xk,--{-X2li-\-...x,la= xh-i,. (7 2)

Выражение (7.2) называют дискретной сверткой входного сигнала и импульсной характеристики фильтра. Определим с помощью соотношения (7.2) сигнал на выходе согласованного фн-Ты-ра. предназначенного для селекции синхронизирующих посылок в виде трехэлементного кода Баркера (рис. 7.7, а). Предположим, что элемент кода задан двумя ныборками, тогда последовательность отсчетов на вхо.де фильтра ПП -1 - 1 (лс = Л = д:2 = л1, XiX; = - \) (рис 7.7, 6). Известно, что импульсная характеристика согласованного фильтра является зеркальным отображением входного сигнала Это означает, что последовательность отсчетов импульсной характеристики -1 - 1 1П1 (h,< = h, = ~\. /i=/ij - - ht = hs-\). ИclHJЛьзyн (7.2), можно записать отсчеты выходного сигнала: i/o = - 1, У] =-2, уг = - 1, уз = 0. уа = 3, у; = 6. Уб = 3. 1/7 - 0, 1/й = - I. f/i = -2, yio= - 1. {Пример вычисления одного lU отсчетов- +л:!*, Н-д:Ло=1 -l-fl- (-1)Н-1-(-1)-1 )

Форма огибающей выходного сигнала и схема фильтра приведены на рис 7.7, я, г. Каскады с коэффициентами передачи -] изменяют полярность отсчетов; узлы фильтра, обозначенные через г", осуществляют сдвиг сигнал:! на один интервал дискретизации, 178

Амплитудно-частотную характеристику Цф определяют, рассматривая его реакцию иа дискретизированный гармонический" сигнал

(д:.) = {Ле"-«), (7.3)

здесь фигурные скобки использованы для обозначения последовательности дискретных отсчетов.

Рис. 7.7. Трехэлементный код Баркера {а); сигналы на входе (б) и на выходе (в) цифрового фильтра; цифровой фильтр (г)

Используя дискретную свертку (7.2) в.ходного сигнала (7.3) и импульсной характеристики фильтра, можно показать, что его передаточная функция

(7.4)

Из (7.4) видно, что КЦт) является периодической функцией частоты с периодом, равным частоте дискретизации [31].

При расчете фильтров широко используют z-преобразование. Если рассматривается последовательность отсчетов сигнала дго, X,, Х2, .... то г-преобраэованием этой последовательности называют сумму

Х(г)-„ + + + ...=

(7.5)

где г -комплексная переменная. Ряд (7.5) сходится при \z\>R, т. е, в области значений, расположенных вне круга радиусом R. Отметим важные свойства г-преобразованмя.

г-преобразоваиие линейно, т, е для носледовательности отсче-1 70в {и,} = {ах + Ьу} можно записать f (г) =(гХ(г)+6 У (2);

символ г"™ служит оператором задержки на m интервалов ди- скретнзации; если дискретная последовательность, г-иреобразова-1 ние которой (2), смешается на ш интервалов дискретизации, то. -преобразование сдвинутой последовательности определяется выражением Y{z)-X {к):

отношение г-преобразовання выходного сигнала фильтра к -г-преобразованию входного воздействия является г-преобразова-нием ею импульсной ларактернстнки

(7.6)1

л называется системной функцией.

Из (7.4) и (7.6) слел1ет, что передаточная функция может С получена из H{z) подстановкой г = е".

Рассмотрим гребенчатый фильтр для разделения гармонических составляющих частоты, которые связаны соотношением = (/г + 0,5)/2, например спек-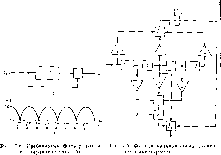

корректора

тров сигналов яркости н цветноепг системы NTSC (рис. 7.8. а). Отсчеты импульсной характеристики определяются единичным в\од1гым нoJЛcГ[cтннeм lOO н задержанным на ;V интервалов дискретизации входным сигналом 00... 01 Так как г-нреобразование цервой последовательности равно единице, второй 2"", то /У (2j = A(l-f .--«). (» = Я(2)!, --------"

..--.Л(1 ]-е-/")-2Ле,