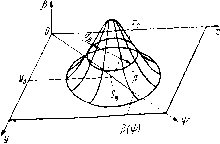Рис.

10.3. Модель исследуемого изображения

ент отражения). Центральная часть объекта, как видно из рис. 10.J, обладает большим коэффициентом отражения, чем периферийная. Зависимость р(д-, у) создает картину изображения объекта при визуальном исследовании и является предметом измерений прн количественном анализе.

Измеряемыми параметрами изображения являются размер площадь Sf, и периметр Гр объекта исследований в пределах видимого контура или на заданном уровне коэффи-ента отражения р, как указано на рис. 10.3, максимальный коэффициент отражения Ртах, зависимость величины Р вдоль выбранного направления, например р (iji) (фотометрическая кривая), координаты лго, Уо объекта в поле изображения и др.

В ряде случаев в качестве измеряемых параметров

используют проекции линейных размеров исследуемых объектов на координатные оси плоскости сканирования, коэффициент формы Гр/5ц и др.

Измерение перечисленных параметров фрагментов изображения

основано на использовании функциональной связи между этими параметрами, временными и амплитудными характеристиками сигналов изображений. Как видно из рис. 10.4, координата Хи левой границы объекта в строке i связана с временным положением tu фронта сигнала изображения, соответствующего этой строке растра, соотношением X\i = = vJu, где t):t -скорость перемещения сканирующего элемента в плоскости изображения в направлении оси X. Соответственно координата хц правой границы X2i = Vxt2i, а размер объекта в этой строке (размер хорды) li=X2i-ДГи = = Vx{t2i--t\i)=VKT.u где Tj -длительность импульса, сформированного в строке i растра.

Таким образом, измерение длительности временного интервала Тг приводит к определснию длины отрезка /, при заданных скорости развертки Vx и коэффициенте увеличения оптической системы. Не-

Рис. 10.4. К принципу измерения размеров объектов

трудно видеть, что часть площади S, объекта в строке сканирования i составляет Si = lig(, = Vxg(,ri, где g(, - щирина строки (расстояние между смежными строками). Площадь всего объекта может быть

определена как S = Vxgd т,, где (=1-строка, соответствующая

пересечению сканирующим элементом исследуемого объекта; п - полное число строк растра, перекрывающих этот объект.

Следовательно, измерение координат и длины прямолинейных отрезков в направлении сканирования, а также площадей объектов

сводится к измерению длительно-

му ft)

св -1

сти сигналов изображения в направлении сканирования. Измерение координат и длины прямолинейных отрезков в направлении вертикальной развертки (оси у) сводится к определению числа строк растра, перекрывающих со-Рнс. 10.5. Функциональная схема ответствующий линейный отрезок, измерения размеров Рассмотренные принципы из-

мерений могут быть реализованы с помощью функциональной схемы, показанной на рис. 10.5. Сигналы изображения u(t) поступают на пороговое устройство (П), формирующее двоичный сигнал, соответствующий заданному уровню коэффициента отражения р, и далее на схему выбора (СВ) измеряемого фрагмента изображения. При измерении размеров эта задача рещается с помощью генератора Fi прямоугольных импульсов, фиксирующих на экране видеоконтрольного устройства строку (например i, как показано на рис. 10.4) и ориентировочные координаты измеряемого отрезка, а при измерении площадей - «зону интереса», охватывающую весь интересующий исследователя объект. Выбранная указанным способом последовательность прямоугольных импульсов при измерении горизонтальных размеров и площадей сопоставляется в логической схеме И с последовательностью калиброванных по частоте следования счетных импульсов, поступающих с выхода генератора Гг. Таким образом число импульсов, поступающих на счетчик (Сч) импульсов, оказывается пропорциональным длине измеряемого отрезка /, или площади 5 выбранного фрагмента изображения.

При построении измерительных систем решающее значение приобретают вопросы обеспечения требуемой точности измерений.

Топологические характеристики. Топологическими называются свойства, инвариантные к так называемым резинообразным преобразованиям. Если представить плоскость изображения в виде резиновой пленки и после формирования на ней изображения подвергнуть пленку деформации, то топологические характеристики объектов и всего изображения не должны изменяться независимо от вида деформации. Очевидно, что такие характеристики, как размеры,

расстояния, углы, площади, не могут быть отнесены к топологическим. К топологическим относятся такие характеристики, как число объектов в заданном поле сканирования, связность и соответствующее число одно-, двух-, трехсвязных и т. д. объектов, число пересечений и др.

Важнейщей топологической характеристикой является связность. В теории распознавания образов связным компонентом множества считают такое его подмножество, в котором любые две точки могут быть соединены кривой, целиком принадлежащей подмножеству. По принципу связности фактически формируется представление об отдельном объекте в поле изображения. В подмножестве связных компонентов могут быть объединены эле- . менты изображения по признаку пре-выщения заданного порога яркости (формируются изоденсы - линии рав- 1+3 ной яркости), по признаку равной цвет-ности и т. д. В качестве примера на l+5 рис. 10.6 представлено изображение с объектами, сформированными из трех

связных компонентов: а, Ь и с (фон). Р"- JP,"„"з""У

Если выделенное подмножество включает другие связные компоненты,

то их называют дырами этого подмножества; любой элемент дыры находится внутри выделенного подмножества. Если выделенное подмножество связное и не имеет дыр, его называют односвязным; при наличии дыр подмножество называют многосвязным.

Топологические характеристики используются при описании объектов в качестве признаков для их классификации, в системах распознавания образов и др. Для рещения указанных задач топологические характеристики используются совместно с метрическими, а в некоторых случаях - и с динамическими.

Если трудности, возникающие при измерении метрических характеристик, при определении топологических параметров снимаются полностью (например, влияние нелинейности сканирования) или существенно снижаются (например, влияние нелинейности амплитудных характеристик системы), то возникают значительные проблемы, связанные непосредственно с самой природой дискретности растра как в вертикальном, так и в горизонтальном направлении (в случае использования двумерной дискретизации изображения).

При сканировании изображения от каждого выделенного по связности объекта формируется несколько импульсов сигнала изображения (в различных строках). Число этих сигналов определяется соотнощением размера объекта и щага разложения. Больщин-ство известных методов счета объектов основаны на использовании принципа распознавания сигнала «первой встречи» разлагаю-