щего элемента с объектом и автоматического счета этих сигналов, число которых оказывается равным числу объектов в поле изображения.

Для объектов сравнительно простой формы (круглых, оваль-лых, прямоугольных и т. п.) задача решается путем сопоставления временного положения видеоимпульсов в смежных строках. Равенство с заданной точностью моментов начала и конца видеоимпульсов свидетельствует о том, что эти сигналы порождены одним объектом и могут быть исключены из счета. Сигнал «первой встречи» разлагающего элемента с объектом распознается по признаку отсутствия сигнала с близкой по значению координатой (во временной области) в предыдущей строке. Такой сигнал подается на счетчик.

Изложенное иллюстрирует рис. 10.6, где сигналы изображения, соответствующие строкам i, i+l, i+2, условно показаны штриховыми линиями. Сопоставление сигналов строк i и i+ \ свидетельствует об отсутствии корреляции во временном положении импульсов смежных строк (в этом случае сигнал поступает на счетчик импульсов). Сопоставление сигналов последующих смежных строк i+l и 1 + 2; 1 + 2 и i + 3, ... показывает существенную корреляцию за временном положении видеоимпульсов, что свидетельствует о принадлежности этих сигналов одному объекту (такие сигналы счетчиком не регистрируются). Таким образом, счетчиком импульсов регистрируется только сигнал «первой встречи», т. е. каждый объект в поле изображения. Для формирования одновременных сигналов смежных строк в системах с построчной разверткой используют цифровое запоминающее устройство с емкостью, соответствующей числу элементов изображения в одной строке.

Измерение динамических характеристик. К динамическим характеристикам относят скорости перемещения объектов в поле изображения, направления перемещения и траектории движения объектов, распределение скоростей в потоках движущихся объектов, динамику изменения размеров фрагментов, а также окраски объектов и др.

С изучением динамических характеристик связан анализ движущихся объектов как черно-белых, так и цветных изображений. Примерами таких изображений и задач измерения их динамических характеристик могут служить: изучение скоростей и траекторий движения кровотока в микрососудах, измерение скоростей и взаимных траекторий перемещения транспортных средств, перемещения участков отдельных органов в рентгенодиагностике и др.

Ряд методов, используемых в сканирующих системах для измерения скоростей движущихся объектов, основан на корреляционных принципах измерения. Эти методы явились естественным развитием принципов измерения, использовавшихся в одномерных устройствах. В системах, основанных на измерении взаимокорреляционной функции, путем стробирования сигналов изображения исследуются два фрагмента изображения, расположенные один за другим в направ-

лении перемещения изучаемых объектов в поле сканирования (/ и 2 на рис. 10.7, а). Сигналы и u2{t), соответствующие выбран-

ным фрагментам, поступают на коррелятор, который вычисляет взаимную корреляционную функцию

Щ {t -x)u2(,t)dt,

где т - время задержки сигнала U\(t).

Если сигналы «1 (О и «2(0 соответствуют стационарному случайному процессу, то максимум взаимной корреляционной функции Tmax = c?/f, где d - расстояние между выбранными фрагментами; V - скорость движения потока объектов (или поверхности объекта) (рис. 10.7, б). Таким образом, измерение величины Ттах приводит к определению скорости движения одиночного объекта или потока частиц в выбранном направлении.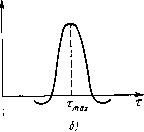

Рис. 10.7. К принципу измерения скоростей объектов

Методы, аналогичные рассмотренному, используются в устройствах для измерения скорости потока крови в микрососудах.

В случае измерения текущих значений скоростей и направлений движения квазиоднородных потоков могут быть использованы взаимокорреляционные методы измерения с тремя выбранными фрагментами стробирования {1-3 на рис. 10.7, а) с целью измерения составляющих вектора скорости Vx и Vy, последующего определения текущего значения скорости у и ее направления в плоскости сканирования.

Для измерения скорости перемещения неоднородных потоков используется метод, основанный на измерении корреляционной функции сигнала и его спектральной плотности.

Измерение характеристик цветных изображений. Как было показано в гл. 2, цвет может быть представлен вектором в некотором трехмерном пространстве, называемом цветовым пространством. В процессе анализа и проектирования телевизионных систем для

оценки цветности частот используют колориметрическую систему преобразования изображения. Координатами цветности в такой системе являются величины

"1

Ul + U2 + «3

п = -

"2

"1 -Ь "2 + «3

которые определяются цветоделенными сигналами U\, «2 и «3.

Сформируем в плоскости цветового графика прямоугольное окно вида

Yj{m, п)=f\{a{jUi{m, п)-\-аф2(т, n)-\-aT{т, л)>01=1,

где через [Рг/\ обозначено отображение, которое ставит в соответствие истинным предикатам Рг/ некоторую функцию Yj{m, л) = 1, а ложным Yj{m, «)=0; ац\ а2/, аз,* - коэффициенты, определяющие координаты и размер окна Я/; «i(m, п), ич{т, п), Т{т, п) - цветоделенные сигналы и модуль цветности, соответствующие элементу изображения с цветностью т, п.

f(i,y) Yj(x,y)

Подпрограмма

"МетрикГУ- WU), mS), WfH

-(шопогия-* W(KI, W(q)

-». -jHamiH-*

W(L)

W(m,n)

Рис. 10.8. Алгоритм анализа цветных изображений

Указанная процедура - цветовая фильтрация - реализуется с помощью цифрового фильтра, на выходе которого в процессе сканирования формируется двоичный сигнал Yj{t), причем У/() = 1 в моменты времени, когда сканируемый участок изображения имеет цветность, принадлежащую окну Я/, и Yi{t) =0 во всех других слу-