равных количествах получают белый, называют яркостными коэффициентами.

Цветовое пространство, цветовая диаграмма. Цветовое уравие-1Ше (2 15) показывает, что цвет может быть представлен как вектор трехмерЕюго пространства. Проекции вектора на оси координат, задаваемые единичными векторами R, G и В. соответственно равны r, g, в. Если ввести обозначения r = ol/or, g = om/og, в = = on/ob и построить систему цветовых координат на единичных: векторах R. G, В, то векторное представление о цвете можно проиллюстрировать рнс. 2.15 {на рисунке концы векторов R, G, В, S имеют те же обозначения, что и сами векторы). Каждому цвету соответствует точка пространства, определяемая вектором (например, точка S). Таким образом, можно построить некоторую систему классификации цветов. Пространство н выбранной системе координат называют цветовым пространством.

Очевидно, что сложение любых двух цветов не может привести к «чер- Рнс 2 15. К определению цве-ному» {отсутствие излучения), поэтому тового пространства

все цветовые векторы должны располагаться в пределах телесного угла, меньшего 2л. Это свойство должно учитываться при выборе системы цветовых координат.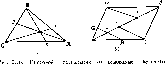

Рассмотрим основные свойства цветового пространства. Соединим точки R, G. В (см. рис. 2.15) прямыми и получим некоторый треугольник ygb - цветовой треуго.гьник. Любой вектор {например, S) пересекает плоскость, в которой расположен этот треугольник Следовательно, каждому вектору на плоскости RGB соответствует единственная точка (например, точка f на рис. 2.15 и 2 16. с), которая однозначно определяет положение вектора (S).

Определим положение этой точки через модули цветов. Для этого проведем прямые RF, GF. BF и найдем положение точек d,

я и к пересечения этих прямых со сторонами треугольника RGB. На рис. 2.16, б изображено основание фигуры, приведенной на рнс. 2.15; M/GR и el\\or. Тогда el/kr=ol/on.r, M/MG = = om/oog. Следовательно, el = kr(r), mi=kg(g}. Учиты-вая, что el-=mj. имеем

kr!k( = g;r. (2,!6а)

Аналогично можно показать, что

ия (2.166), dudg = 0,b. {2,16в)

Соотношения (2.16) определяют положение точек я. к п о через модули цветов Нетрудно видеть, что полученное правило (2.16) соответствует правилу отыскания центра тяжести треугольника с грузами, сосредоточенными в его вершинах и равными r, g и в соответственно.

Произведем нормировку йо компонейам смешиваемых цветов:

л + а + i

(2.17

Видно, что r-t-g-f = 1-

Нормированные компоненты г, g, ь определяют соотношения количеств трех основных цветов, при которых они воспроизводят данный цвет. Oihi не содержат информации о модуле цветового вектора, но в них полностью сохранена информация о его направлении. Точку пересечения вектора цвета с плоскостью треугольника RGB называют точкой цветности (точка f на рис, 2.15 и 2.16. а) или просто цветостью. Отличия цветности, фиксируемые 8 экспериментах с гипсовой призмой, отражают различия в цветовых ощущениях наблюдатели, т, е термин «цветность» предполагает корреляцию с ощущением цветовых различий (ощущением цветности) .

Компоненты г, g, которые полностью определяют цветность, называются трехцветными, коэффициентами или координатами лветности. Задавая две из них, как Biuiro из соотношения (2,17). Л10ЖНО однозначно определить цветность.

Таким образом, любой цвет в выбранной системе координат выражается тремя числами - модулями цветов, цветность же определяется любыми двумя числами из тре.; г, g. h.

Эксперименты по уравнению цветов измеряемого и эталонного источников, описываемые уравнением (2.15), могут быть повторены для всех моно.роматическнх излучений видимого спектра.

Результаты статистических исследований подобных характеристик цветового Зрения человека приводят к зависимостям г, g, ь от Я, (рис 2 17). Из них видно, например, что для получения ощущения, эквивалентного вызываемому монохроматическим излучением с длиной волны Л = 500 нм. необходимо смешать выбранные основные цвета в соотношении Ь = 0.78; g=l,;19; /= - 1,17, Аналогично с помощью кривых смешения могут быть определены необходимые

соотношения г, g н b для любого монохроматического излучения.

Нанесем на плоскости цветового треугольника линню. соответ-ствуюш,ую монохроматическим цветам (линию чистых спектральных цветов). Для этого воспользуемся экспериментальными кривыми смешения (см. рис. 2.17). Например, для 1500 км имеем g = 1,39; b=0,78; ="-l,17, Воспользовавшись правилом (2,16), най-дем положение точки л, соответствующей /, = 500 нм (рис, 2,18). Аналогично можно найти точки для других длин волн н соединить их в непрерывную кривую чистых спектральны.ч цветов RG/1B, Белый цвет, соответствующий равноэнергетическому в пределах ви-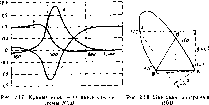

димого спектра излучения, отображается точкой £ (r = g=&= i/3). Штриховая линия RB - линия смеси красных и синих цветов - пурпурных цветов. Все остальные цвета, отличные от чистых спектральных н чистых пурпурных цветов, лежат внутри построенной кривой rgab. Таким образом, поЛученэ цветовая диаграмма RGB, в которой любой цветности соответствует единственная точка (иногда эту диаграмму называют цветовым графиком). С помощью цветовой диаграммы можно коли1!ественно (в виде координат точки) опреде-

1 лнт[1 любые цветовые отличия, воспринимаемые человеческим гла-

1 зом при воздействии излучения.

Из Уравнения (2.15) видно, что в процессе установления модулей цветов для получения заданного цвета смеси яркости получаемых цветов различны (они определяются яркостями источников основных цветов и соотношением модулей цветов для данной смеси).

Уравнение (2.)5) после нормировки для любого монохроматического излучения можно записать в виде

(2,18)

Если мощность результирующего излучения смеси обозначить pi, и разделить обе части уравнения (2.18) на эту величину, то получим