
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) ( 43 ) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (43) нале равном нулю. Смысл применения оценки (8.31) заключается в том, что интеграл находят без вычисления подынтегрального выражения. Чем меньше интеграл, тем выше качество работы системы РА и наоборот. Интегральную оценку (8.31) называют первой интегральной оценкой. Для ее расчета необходимо в преобразовании Лапласа для y{t) при заданном начальном состоянии положить р=0. Первая интегральная оценка используется только в тех случаях, когда заранее известно, что переходный процесс в системе РА имеет монотонный характер. Ча-Рис. 8.4. К определению сто по значению первой инте-первой интегральной гральной Оценки нельзя судить оценки о качестве работы системы. Дей- ствительно, если в системе РА имеют место незатухающие колебания (рис. 8.4), то первая интегральная оценка окажется равной нулю, т. е. будет соответствовать высокому качеству работы, на самом деле такая система неработоспособна. Поэтому качество работы систем РА определяют с помощью квадратичной интегральной оценки: 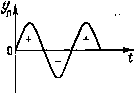 o = jy4t)dt. (8.32) Очевидно, для системы с переходным процессом, показанным на рис. 8.4, квадратичная интегральная оценка равна бесконечности, т. е. соответствует неудовлетворительному качеству работы. Для достижения требуемых показателей качества работы ряд параметров системы РА могут варьироваться относительно расчетных значений. К числу таких регулируемых параметров относится коэффициент усиления системы, постоянные времени корректирующих устройств и другие значения параметров, при которых интегральная оценка имеет мини.мальное значение, называют оптимальными. Оптимальные параметры находятся из следующей системы уравнений: J = 0, /=1,2,...,й, (8.33) где р, - регулируемые параметры; А -число регулируемых параметров. Иногда выбор параметров из условия минимума оценки (8.32) приводит к резко выраженным колебательным процессам, поэтому в системах РА применяется обобщенная интегральная квадратичная оценка: J = ]v(t) dt. (8.34) где v(t) -квадратичная форма. Примером квадратичной формы является функция Vи) = а, г] (О + «2 4(i) 1 (О, (8.35) где 2i(/), 2(0, Zn{t) - составляющие вектора состояния; а; - весовые коэффициенты. В простейшем случае интегральная оценка (8.34) имеет вид (8.36) где т - весовой коэффициент. Физический смысл интегральной оценки (8.36) следующий. При выборе параметров системы РА из условия минимума оценки (8.36) не допускается как длительное отклонение от нуля переменной (иначе первая составляющая оценки будет большой), так и большое значение гг{1) (иначе вторая составляющая оценки будет большой). Таким образом, получается хотя и быстрый, но и плавный переходный процесс. При этом, чем больше весовой коэффициент т, тем более медленному переходному процессу соответствует минимум интегральной оценке (8.36). Оказывается, что выбор параметров системы РА из условия минимума оценки (8.36) означает приближение переходного процесса в системе к экспоненте с постоянной времени т, а из условия минимума оценки (8,32) - приближение переходного процесса к ступенчатой функции. Для вычисления квадратичных интегральных оценок выражение (8.35) необходимо записать в матричном виде (см. приложение П.4): v{t)V (t)\Z[t), (8.37) -а„ О, О,..., 0-0, а, О,..., О 0, О, О,..., а„ - матрица квадратичной формы. Расчет квадратичных интегральных оценок основан на введении дополнительной квадратичной формы, которая с квадратичной формой интегральной оценки (8.35) связана выражением -fw(t)=-v(t). (8.38) При этом квадратичная интегральная оценка (8.34) принимает вид = - -~-w(t)dt = wiO). (8.39) Если выразить дополнительную квадратичную форму через вектор переменных состояния (0 = Z(OWZ(/), (8.40) то (8.39) окажется следующей: yv, = Z(0)WZ(0), (8.41 где W-матрица дополнительной квадратичной формы; Z(0)-начальное значение вектора переменных состояния. Для определения матрицы дополнительной квадратичной формы подставим выражение (8.40) в (8.38). В результате найдем, что -- ш (О = Z" (О WZ (О + Z (t) WZ (О - - Z (t) VZ (t). (8.42) Учитывая векторное дифференциальное уравнение системы (8.8), в котором x(t)=Q, получим ZJ (t) WZ (О + Z" (О WAZ (О = - Z (t) VZ (t). (8.43) Из этого выражения следует матричное уравнение AW+WA -V. (8.44) К сожалению, из последнего уравнения нельзя в общем виде определить матрицу W. Поэтому поступают следующим образом. Выполняют операции умножения и сложения в левой части уравнения (8.44), после чею приравнивают элементы полученной матрицы к соответствующим элементам матрицы справа. Так как матрица W - симметричная матрица, то в результате получают си- (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) ( 43 ) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) |
|
|