ет связь выходного сигнала системы с вектором переменных состояния.

Так же как и в непрерывных, выбор переменных состояния в цифровых системах является неоднозначной операцией, т. е. векторное разностное уравнение зависит от выбранных переменных состояния. Однако все возможные векторные уравнения эквивалентны, так как описывают один и тот же динамический процесс связи выходного сигнала системы с входным. Проиллюстрируем это на конкретном примере.

Пример 11.1. Найти векторное разностное уравнение для системы, дискретная передаточная функция которой

г?-0,7бг-Ь 0,125

Решение. Данной передаточной функции соответствует разностное уравнение

j/(n-f2)-0,75г/(п-Ь 1)-Ь0,125г/(п) =а:(п-Ь 1)-х(п). На основании выражений (11.4), (11.7) получим, что

- 0,125,

+ 0,75

0,25

Уравнения системы в пространстве состояний получаются следующими:

gi{n+l)=g2{n)+x(n); (11.8)

§2 (" + 1) =- 0,1.25gi (п) + 0,75g2 (п) - 0,25а; (п), а уравнение выхода имеет вид

J/(n)=gi(n). (11.9)

На рис. 11.2, а изображена структурная схема рассматриваемой системы, построенная по уравнениям (11.8) и (11.9), из которой видно, что переменные состояния - это сигналы на выходах звеньев запаздывания.

Представим передаточную функцию системы в виде

г-0,25 ~ г-0,5 "

Такой передаточной функции соответствует структурная схема, приведенная иа рис. 11.2,6. Выберем в качестве переменных состояния сигналы на выходах звеньев запаздывания. Тогда можно записать следующую систему уравнений:

fi {n+l) = 0,25fi(n) + 3x(n);

/(n-f 1) =0,5/з(п)-2л:(п). (11.10)

В этом случае уравнение выхода имеет вид y{n)=h(n)+f («)

(11.11)

Перепишем выражения (11.10) и (11.11) в матричной формег F(n+l) = \pF(n) + BpX(n)i (/(n) = CF(n),

/1 (n)

где F(n) =

L/2 in) J

- вектор переменных состояния;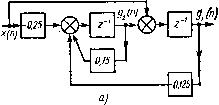

xfn)

0.25 J

-2 -HRK 2"

0.5 -i

Рис. 11.2. Схемы системы второго порядка:

а - относительно дискрет выходного сигнала; б - относительно полюсов системы

0,25, О О, 0,5

Из уравнений (11.8) и (11.10), (11.9) и (11.11) следует, что различным переменным состояния соответствуют различные матрицы системы, управления и наблюдения, но связь выходного сигнала системы с входным остается неизменной:

j/(n) = CG(n) = CF(n).

Ранее цифровые системы РА в пространстве состояний описаны для стационарных систем. В нестационарных системах матрицы системы управления и наблюдения являются переменными, и векторные разностные

уравнения имеют такой вид

С(л+1) = А(и)0(«)4-В(/г)д;(п); (11.12)

y(n)=C(n)G{n) + ho{n)x{n). (11.13)

В общем случае цифровая система имеет г входов и m выходов. При этом вид векторных разностных уравнений остается таким же, как и в (11.12) и (11.13), в которых Матрица системы А имеет тот же вид, что и в системах с одним входом, и одним выходом, изменяются лищь матрицы управления и наблюдения. Матрица управления становится прямоугольной размером lydr, а матрица наблюдения имеет размер /X"-

§ 11 2. ДИСКРЕТНАЯ МАТРИЦА ПЕРЕХОДА

Рассмотрим однородное нестационарное уравнение, которое получается из разностного векторного уравнения (11.12) при д;(п)=0:

G(n+1) = A(rt)G(«). (11.14)

Обозначим через G(0) начальное состояние системы. Тогда из выражения (11.14) последовательно получаем:

G(1) = A(0)G(0);

G(2) = A(1)G(1) = A(1)A(0)G(0); (11.15)

G(n)= Г1 A(/)G(0).

Введем дискретную матрицу перехода с помощью соотношения:

G (я) = Ф (и, т) G (т).

Дискретная матрица перехода Ф{п, т) обладает следующими свойствами:

Ф(п,«) = 1; Ф(п,т) = 1Ф{т,п)]-\

где I -единичная матрица.

Соотношения (11.15) через введенную дискретную матрицу перехода записывают в виде

С(п) = Ф{п, O)G(O). Тогда матрица перехода имеет вид

Ф(п,0)= П А(0. (11.16)