
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) ( 73 ) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (73) которого имеет такой вид: G(tt+ 1) = Ф(п+ 1,«)0(«) + В(/г+ l)V(n); X(n+l)=C(n + l)G(n+l), (11.25) где О («)-вектор переменных состояния сигнала; Ф(«+1, п) -дискретная матрица перехода; В{п+1) - матрица управления; С(«+1)-транспонированная матрица наблюдения. 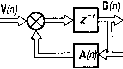 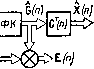 Рис. 11.3. К постановке задачи дискретного фильтра Калмана Гауссовская случайная последовательность V(tt) имеет характеристики M[V(tt)]-0; iM[V(tt)V"(/)]=Q(tt)6„;, (11.26) где Q(tt) - матрица интенсивностей белых шумов на входе формирующего фильтра вектора сигнала; 1 при « = /; О при п Ф ], М означает взятие математического ожидания от выражения, заключенного в квадратные скобки. Начальное состояние вектора переменных состояния G(0) характеризуется гауссовским распределением с характеристиками Af[G(0)] = 0, Af[G(0)G"(0)] = R£(0). (11.27) Измеряемый сигнал (воздействие на входе синтезируемого фильтра) F (п) = С" («) G («) + N (п), (11.281 где N(tt) -вектор помех с характеристиками. При этом M[N(n)] = 0; M[N(tt)N(/)] =Р(«)б„;, (11.29) где Р (п) - матрица интенсивностей белых шумов вектора помех. Случайные последовательности \ (п) и N[nJ полагаем некоррелированными. Задача синтеза состоит в том, чтобы найти векторное разностное уравнение фильтра, обеспечивающего по измеренным значениям сигнала (11.28) F(l), F(2), F{n) оптимальную текущую оценку вектора переменных состояния сигнала с минимальной дисперсией ошибки: М[ЕГ{п)т(п)] = тт, (11.30) где Е(«) =G(tt)-G(«/«)-вектор ошибки; G(n/n)- оценка вектора переменных состояния сигнала. § 11.4. ДИСКРЕТНЫЙ ФИЛЬТР КАЛМАНА Найдем векторное разностное уравнение оптимального фильтра Калмана. По определению оценка вектора переменных состояния сигнала определяется выражением [10] G(rt4- 1/П+ l) = iM[G(tt+ 1)/F(1),F(2).....F(n + 1)]. (11.31) Введем с помощью соотношения F = («-Ь 1/«) = F(tt Ч- l)-M[F(tt-Ь 1)/F(1),..., F(tt)] (11.32) невязку измеряемого сигнала (11.28). Принимая во внимание, что математическое ожидание F{j) равно нулю, выражение (11.31) перепишем в виде G{n + Un+ l) = M[G(tt+ 1)/F(1), F(2),...,F(rt)]-}-- М [G (п + 1)/F (п + 1!п)] = G{n + 1/п) + + M[G(n+1)/F(rt+1/rt)]. (11.33) Так как G{n-\-l) и Р(«+1/«) -гауссовские последовательности с нулевыми математическими ожиданиями, то второе слагаемое в выражении (11.33) можно записать так: М lG{n + 1)/F {п + 1/п)] = R R- f{n+ l/n), (11.34) где R = М [G (n + 1) F {n + l/n)], R = M lf(n + + l/rt)F(tt+ 1/tt)]-матрицы корреляционных моментов. 15-493 225 Введем матрицу усиления K(«+i) = R,R~~- (11.35) Учитывая, что 0(п + 1/п) = Ф{п+ l,n)G (п/п), выражение (11.33) представим в виде G(n+ 1/П + 1) = Ф{п+ l,n)G{n/n) + K{n+ l)F(rt+ \/п) (11.36) Первое слагаемое в этом выражении определяет оценку в момент времени t- («+1)Г по результатам п измерений, второе уточняет эту оценку по последнему измерению. Измеряемый сигнал характеризуется выражением (11.28). Невязка этого сигнала (11.32) некоррелирована с вектором помехи N{n), поэтому выражение (11.32) можно записать так: Р{п+ lfn) = F(n + 1) - С{п + l)G(n+ l/rt) = = F{n+ l) - C(n+ 1)Ф(п+ 1, n)G{nfn). (11.37) Подставив (11.37) в уравнение (11.36), найдем, что G{n + \/п+ 1) = Ф(/г4- l,n)G{nln) + Kin+ l)[F(n + + l) - C{n + 1)Ф(д + l,n)G{n/n)]. (11.38) Выражение (11.38) является векторным разностным уравнением оптимального фильтра, в соответствии с которым на рис. 11.4 построена структурная схема фильтра. Из этой схемы видно, что найденный оптимальный фильтр -это система с обратной связью, внутренним контуром которой является формирующий фильтр сигнала, а параметры обратной связи определяются матри. цей усиления. Найдем эту матрицу. Для этого подставим в выражение (11.37) вектор (11.28). В результате получим F{n+ 1 г) = €(«+ l)G{n+ l) + N(/i+ i)-C(n + 1)х X G(n+ lln)(f(n+ l)E(n+ l/n) + N(fi+ 1), (11.39) где Е(л + l/n)=G{n + l) - G(n+ l/n)- вектор ошибки. (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) ( 73 ) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) |
|
|