
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) ( 83 ) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (83) четы провести для случая, когда cf(t)=ixt, а-0,7 рад-с-, а передаточная функция исполнительного устройства системы (р)=къ1р, где и=0,35 рад/(с-В). Решение. Спектральная плотность помехи, действующей на вход системы, 5л (ш) = 1 +0) где Л?п = 0,3-10- радС; Тп=0,05 с. Пеленгациоиная характеристика системы сопровождения аппроксимируется выражением (12.21), в котором А = 5 В; а=0,314. Уравнения (12.22) и (12.23) для рассматриваемой системы получаются следующими: 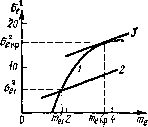 (12.24) 2r„(l-i-fti (/n,ae)U (12.25) Расчет коэффициентов статической линеаризации выполним в такой последовательности. Проведем на 12.10, а прямую, уравнение которой следует нз выражения (12.24) и имеет вид feo {т, а,) me = = 2В. (12.26) По точкам пересечения этой прямой с изображенными на рис. 12.10, а кривыми найдем зависимость (кривая ) на рис. 12.12) Рис. 12.12. К вычислению коэффициентов статистической линеаризации в системе автосопровождения цели (12.27) Формула (12.27) связывает математическое ожидание сигнала ошибки и дисперсию этого сигнала а», удовлетворяющие уравнению (12.26). Для каждой пары значений и а], связанных уравнением (12.27), по формулам (12.20) рассчитывают коэффициенты статистической линеаризации к, а по формулам (12.25) - зависимость дисперсии сигнала ошибки а\ от математического ожидания этого сигнала (кривая 2 на рис. 12.12). Точка пересечения кривых / и 2 и определяет математическое ожидание сигнала ошибки и дисперсию этого сигнала a. В рассматриваемой системе автоматического сопровождения цели /Пе1 = 3,1410-2 рад; а, =1,5-10-з рад. По этим значениям и кривым рис. 12.10 находят коэффициенты статистической линеаризации о=64 В/рад; 12=57,3 В/рад, которые затем используют для оценки точности работы системы. Динамическая ошибка системы определена - это значение математического ожидания сигнала ошибки тц. Дисперсия ошибки системы из-за действия по- мехи, согласно (6.20), = 1,5.10-3 рад, где I Wijw) I - АЧХ замкнутой системы. Таким образом, суммарная средняя квадратическая ошибка системы автоматического сопровождения цели <s=Kl+L)" = 5-10- рад. Определим условия, при которых в следящей системе из-за не-лш!ейных свойств пеленгационной характеристики происходит срыв сопровождения цели. Процесс срыва носит случайный характер, поэтому его характеристикой является вероятность возникновения срыва за какой-то промежуток времени. Вычисление этой вероятио-стн является сложной задачей. В инженерной практике ограничиваются выявлением характеристик сигнала и помех, при которых происходит срыв сопровождения цели. Метод статистической линеаризации позволяет решить эту задачу, при этом удобно использовать графический способ, который применялся ранее для анализа стационарных режимов в системах РА. Оценим, при каком уровне спектральной плотности помехи происходит срыв сопровождения цели в системе, рассмотренной в примере 12.2. С увеличением уровня спектральной плотности помехи кривая 2 на рис. 12.12 не изменяет своей формы и смещается вверх; при каком-то значении Лп кривые / и 2 не будут пересекаться. Это означает, что отсутствует совместное решение уравнений (12.24) и (12.25). Математическое ожидание и дисперсия сигнала ошибки резко возрастают и происходит срыв сопровождения цели, система становится разомкнутой, а следовательно, неработоспособной. После срыва сопровождения цели математическое ожидание сигнала ошибки неограниченно увеличивается, а дисперсия сигнала ошибки оказывается равной дисперсии помехи. Граничное значение уровня спектральной плотности помехи Лп, прн котором происходит срыв сопровождения цели, равно Лпгр. При этом кривая 2 на рис. 12.12 оказывается касательной к кривой/. В рассмотренном ранее примере Лп гр= =9,14-10-* рад-с. Граничное значение уровня спектральной плотности помехи зависит от параметров системы, управляющего воздействия и ширины спектра помехи. Так, с ростом производной управляющего воздействия увеличивается математическое ожидание сигнала ошибки, в результате чего .Vn гр уменьшается. С расширением спектра помехи .Vn гр также снижается, так как при этом увеличивается дисперсия сигнала ошибки. С ростом коэффициента передачи линейной части системы сигнал ошибки уменьшается, а следовательно увеличивается Лп гр. § 12.7. ПРИМЕНЕНИЕ ТЕОРИИ МАРКОВСКИХ ПРОЦЕССОВ ДЛЯ АНАЛИЗА НЕЛИНЕЙНЫХ СИСТЕМ Некоторые задачи анализа систем РА могут быть решены, если использовать методы, разработанные для исследования марковских процессов, отличающихся от дру- гих случайных процессов простотой статистической связи между предыдущими и последующими значениями случайного сигнала. Случайные процессы характеризируются «-мерной плотностью распределения вероятности w(X\, Xi, Хп), где Xx=Xx{tx)\ Х2=Х2{к)\ Xn=Xn{tn). Через условную плотность вероятности, характеризующую распределение x(t) в момент времени tn при известных значениях х,, Х2, Хп-и «-мерную плотность вероятности процесса x{t) можно записать так: хю{х, х,..., х,) = W(Xi, X,...., w{xjx, x.,... Xn-i). (12.28) Случайный процесс x(t) называют марковским (или процессом без последствия), если для любых « моментов времени ti<z.t2<i...<.tn условная плотность вероятности «последнего» значения Хп при известных Хи х, .... Хп-\ зависит только от Хп-\ и не зависит от всех предшествующих значений, т. е. справедливо соотношение w{xjx, Jfj,...,Ха-\) = w{xjxn-i): (12.29) Таким образом, если известно состояние марковского процесса в настоящий момент времени то его будущее значение в момент времени tn+i не зависит от прошлого состояния в моменты времени tn-u tn~2,.... Из выражений (12.28) и (12.29) следует, что W (Xi, Xz,..., Х) = W (дг1, Xz.....Xn-\)w{xJXn-\) = = W [Х, дга,..., Хп-.2) W {Xn-\JXn-2) W (xJXn-l) = = W {Х{) W (X/Xi).. .W {xJXn-l), t. e. «-мерная плотность вероятности марковского процесса полностью определяется одномерной плотностью и плотностью вероятности перехода w{Xi/Xi-i). В [12] показано, что процесс Хи лгг, Хп является марковским, если составляющие х,- удовлетворяют следующей системе стохастических уравнений: = Gj (Xi, 2,..., Х„) + bij (Xi, Xz,...,X„) Ij (t); f-1,2,...,«, (12.31J где Ui - известные нелинейные функции; /(0 -незави! симые белые шумы с единичными спектральными плотно стями No. Плотность вероятности «-мерного марковского прс (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) ( 83 ) (84) (85) (86) (87) (88) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) |
|
|