
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) ( 88 ) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) (88) Пример 13.1. Определить алгоритм оптимального управления для системы, передаточная функция объекта управления которой Wo{p) = z=bo/iP+Oip). Такую передаточную функцию имеет, например, разомкнутая система ФАПЧ без фильтра нижних частот. Решение. Данной передаточной функции соответствует система уравнений в пространстве состояний: gi(0 = g2 (0; giit) =-«1 gi (t)+boU(t). Критерий оптимальности J = \[\g\ (О + agf (О + W] d/. Таким образом, в рассматриваемой системе А =
В соответствии с уравнением (13.12) оптимальное управление имеет вид Элементы матрицы усиления в последнем выражении определим из решения системы алгебраических уравнений, которая получается из уравнения (13.11): 12 "22*0/9; *12 = *21 = /9/*о; «121 + 12 2 Передаточная функция оптимальной системы стабилизации hW, (р) 1 + *о (Ki + hi Р) где ku=ba/q. Найдем оптимальное управление для задачи слежения при входном сигнале x{t) - l(t)-l(t-T). Оптимальное управление определяется выражениями (13.9) и (13.15): « (о =- Ihi gi (t) + h g (t)\ + (0 у . Параметр 22(0 рассчитан и соответствии с (13.15) из следующей спстемы уравнений: Ч it) =-2i (/) + (22bllq - aj (о + оу (о, гдел;,(/) = 1(/-Г); л;2(/)=,(0=0. На рис. 13.2 показана структурная схема спроектированной системы, для вычисления 22(0 которой включено вычислительное устройство. Передаточную функцию этого устройства определим из последней системы уравнений: где c = a-kbl/q; ckbllq. Wo(p) "г/ ff/t) Рис. 13.2. Структурная схема оптимальной системы Второго порядка В оптимальных системах стабилизации и слежения, рассмотренных ранее, полагали, что вектор состояния объекта управления полностью известен, т. е. его можно измерить с помощью соответствующих датчиков. В действительности это нереально. Обычно можно измерить только часть переменных состояния или какое-либо их сочетание, при этом измерения содержат случайные ошибки. Кроме того, сама система, как правило, подвержена воздействию случайных возмущений. Таким образом, для формирования оптимального управления необходимо предварительно оценить вектор состояния, что может быть сделано при построении математической модели объекта управления. Для объекта управления, описываемого уравнениями (13.3) оценку состояния можно осуществить в соответствии с математической моделью Й(0 = AG(0 + BU(0, (13.17) где G(t) -оценка вектора состояния Если начальные значения векторов G(0) и G(0) рав- ны, то в любой момент времени G(t) = Q(t). Однакоточ- ное значение G(0) получить невозможно, поэтому оценка G(/) по модели (13.17) дает большие ошибки. Для устранения этого недостатка на вход оценнвателя состояния кроме сигнала U(t) подают сигнал рассогласования YC/j-CGf/), а вместо уравнения (13.17) используют уравнение G (О = AG (t) + L [Y (О - G (01 + BU {t) (13.18) G(0-[A-LC1G(0+ LY(0 + BU(0, (13.19) - вектор усиления оценивателя размером пХт; т - размерность вы.ходного вектора. Составляющие вектора L выбирают lim IG (t)-Q{t)] = 0. t-*oo такими, чтобы (13.20) Если собственные значения матрицы [А-LC] в (13.20) выбрать так, чтобы их вещественные части были отрицательными, то при любых начальных значениях 0(0) обеспечивается выполнение (13.20). После того как найдена оценка вектора состояния объекта управления, можно использовать алгоритм управления, полученный в задачах оптимальной стабилизации и слежения. На рис. 13.3 показана полная структурная схема оптимальной системы стабилизации с оценива- 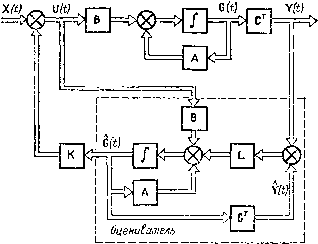 Рис. 13.3. Полная структурная схема оптимальной системы стабилизации (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) (72) (73) (74) (75) (76) (77) (78) (79) (80) (81) (82) (83) (84) (85) (86) (87) ( 88 ) (89) (90) (91) (92) (93) (94) (95) (96) (97) (98) (99) (100) (101) (102) (103) (104) (105) (106) (107) (108) (109) (110) |
|
|