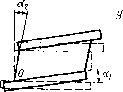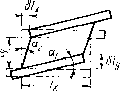Рис, 3,2.

Чтобы различать иаправлеиия действия сил («вдоль» или «поперек» тела), в буквенных обозначениях напряжений п н относительных деформаций е применим двойные индексы. Первым будем указывать направление действия внешней силы F. Силу всегда будем прикладывать так, чтобы она совпадала с направлением одной из координатных осей (х, у, z). Вторым индексом обозначим направление нормали к площадке S, к которой приложено напряжение, Это направлсиие также будем выбирать совпадающим с одной из координатных осей. Так, напряжение, действующее вдоль оси х иа площадке с нормалью в направлении х, обозначаем как их (рнс, 3.1). Теперь напишем формулу для определения коэффпг(,ие1[та Пуассона v, если растяпгвающие напряжения дейс1вуют в паправлепии осп л:

- у.

Относительное сжатие в иаправлеиии осей у а г одинаково. Поэтому одинаковы будут и коэффициенты Пуассона для обоих направлений. Ои будет иметь знак «минус», поскольку деформаиии сжатия, стоящие в числителях формулы (3.1), принято считать отрицательными. Если модуль Юнга у различных материалов может изменяться в очень широких пределах, то коэффи-1шент Пуассона меняется мало.

Теоретически он может изменяться у разных материалов в пределах О.. . 0,5, У болыиниства материалов он равен 0,3 ., . 0,4. И только резина имеет коэффициент Пуассона, близкий к 0,5, а это значит, что ее объем при деформациях почти не меняется.

Мы рассмотрели деформации растяжения и сжатия, при которых форма бруска остается прямоугольной. Если внешние силы действуют не по одной лнннн п

Образуют момент сил, то углы бруска не остаются ирй-Мыми, Такие деформации называют сдвигом, а вызы вающие их напряжения - касательными напряжениями. Чем больше касательные напряжения, тем больше углы [деформированного бруска будут отличаться от прямых углов и тем больше будут деформации сдвига, Поэтому еличнну дсформадш-]" сдвига определяют суммой тангенсов углов aj и «2, показывающих, иа сколько угол 1ри вершине бруска отклонился от прямого угла рнс, 3.2).

xy=eyx=ig Qi+tg 02. (3.2)

Заменив тангенсы углов отношением сторон тре-гольников, можно определить величину деформаций йвига через отношения перемеп!,ений к соогветствую-цим размерам (рнс. 3.2).

Касательные напряжения направлены вл.оль пло-[адки, для которой они вычисляются. Они, например, вляются причиной среза заклепок, соеднняющих ме-аллпческие конструкции. Между касательными иапря-кениями н деформациями сдвига существует прямая [ропорциоиальная зависимость: Сху=Оиху, гд(: коэффн-,иент пропорциональности О называют модулем сдвига.

3.2. Закон парности и сложное напряженное состояние

Для упрои;ения задачи иредиоложим, что касатель-:ые напряжения приложены только к двум граням ре-иновосо куба. В результате создается крутящий мо-кеит, поворачивающий куб, а также нормальные на-1ряжения, не одинаковые в различных точках грани рис. 3,3). Такое состоя[[ие называют сложным напря-кенным состоянием; нам нужно простое наиряжешЕое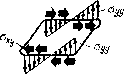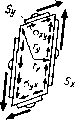

«. 3.3.

Вис. 3,4.

состояние, когда существуют только касательные напряжения. Для этого нужно приложить касательные напряжения еще к двум граням бруса. Крутящие моменты пар уравновесятся н брус разворачиваться не будет, так как действуют только касательные напряжения.

В случае бруска кубической формы касательные напряжения, действующие в 11аиравлеиии д: и у, должны быть равны, потому что только в этом случае создаваемые ИНН моменты будут уравновешиваться. Такое же положение будет, если брусок имеет форму прямоугольного ![араллело![ипсда (рис. 3.4).

Чтобы моменты, создаваемые напряжениями оу и vx уравновешивали Друг друга, необходимо выполнение равенства

где 5ж и Sy - площади граней, а Гд: и Гу - расстояния от нентра до соответствующих граней. Но в недеформированном состоянн]! бруса ry-SJ2h н г-л5у/2Я, где h - высота бруса, поэтому Оху=Оух- Такое же соотношение будет и в деформированном состоянии. Равенство касательных напряжений, действующих по двум взаимно перпендикулярным граням, называют законом парности касательных напряжений,

Распространим наши выводы на обилий случай сложного напряженного состояния, когда действуют все возможные напряжения, К каждой из шести граней бруса приложены три напряжения: одно нормальное и два касательных (рис. 3,5).

Напряжения, действующие по передним граням бруса, будем считать иолом;[гтельнь[.ми, если нх направления совпадают с направлением координатных осей. На-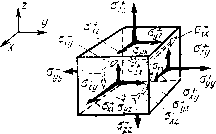

Рис. 3.5.

Пряжения, действующие по задинм граням, условимся считать положительными, если они направлены в сторону, обратную положительному направлению координатных осей.

Напряжения, действующие по противоположным граням, но имеющие одинаковые индексы, дополнительно будем отмечать знаками «плюс» или «минус».

Приняв, что процессы деформирования линейны, найдем общую деформацию, сложив отдельные дефор-ма1[,ин (принцип суперпозиций). Дсформаття растяжения в направлснигг каждой координатной оси определяется прежде всего нормальными [(апряжениями в иа-правленнн этой оси Оуу, U;;. Кроме того, каждое нормальное напряжение вызывает деформацию сжатия в двух других направлениях, поэтому полная деформация растяжения в каждом паправлснии будет зависеть от трех иаиряженин:

1 ч v

а,, -

(3.3)

\ Деформации сдиигов, происходящих в различных

плоскостях, НС влияют друг на друга п не заииеят от деформаций растяжения или сжатия:

--yyJG, s = oJG. (3.4)

х>л

Для расчстои процссеов деформирования конструкций нам потребуется обратная зависимость напряжений от деформаций. Для деформаций сдви[а и касательных напряжешп"] она получается нз уравнений (3.4): ау~

= Gevy, гг.

= G-<

Для получения аналогичной зависимости для нормальных напряжений нужно решить систему (3.3) относительно напряжений. После решения системы и выполнения алгебраических преобразований

XX £2 т гг £2

гг £.

XX £2 ~ УУ £2

+ гг + ) + уу + )]

получим зависимость напряжений от деформаций в виде

Нк (1 - +

(1 - v2)£

(]+v)(l-2v)

(1+v) (l-2v)

+ v) (l-2v)=( + 2)

Яе--,

"yy + SlJ-) Stfl/ + гг

(3.5)

*гг = ( + 21х)е

где X и i -коэффициенты Ламе,

Коэффициенты Ламе выражают через модуль упругости (модуль Юнга) и коэффициент Пуассона

K=Evl{\+){\-2). L-=£/2(l+v).

Коэффициент 1 оказывается равным модулю сдвига G, и для определения упругих свойств материала нам в любом случае нужно знать две характеристики; £" и V или X и 1.

3.3. Трудности при построении модели

Теперь мы можем приступить к построению расчетной модели конструкции. Для этого прежде всего разделяют конструкцию на элементы прямоугольной формы. Для каждого элемента записывают уравнения динамического равновесия и решают эти уравнения на ЦВМ. План простой, но реализовать его трудно. Дело в том, что для получения необходимой точности расчета необходимо разбить конструкцию на большое число элементов. Если, допустим, предстоит рассчитать вибрации блока прямоугольной формы и нас удовлетворяет точность в несколько процентов, то в каждом из трех на-

правлений нужно разделить блок примерно на 10 частей. Таким образом, получится 1000 элементов. Для каждого элемента надо записать три уравнения движения, т. е. решить систему из 3000 уравнений. Наиболее просто решить такую систему можно рассмотренным выше методом последовательных приближений пли методом итерации. Каждое уравнение решают относительно одной неизвестной, при этом необходимо выполнить около 100 элементарных операций. Следовательно, чтобы прорешать один раз все уравнения, необходимо выполнить 300 ООО операций.

При методе последовательных приближений для получения трех верных знаков результата нужно выполнить около тысячи операций. Чтобы получить результаты для всех элементов для одного шага по времени потребуется 300 000 000 (3-10) операций. И такая процедура должна производиться в каждом шаге по времени. Если процесс занимает 1000 шагов, то число элементарных операций на ЦВМ достигнет 3-10.

Как легко заметить, расчет механических процессов в упругих телах требует огромного объема вычислений. Современные ЦВМ среднего класса выполняют в секунду 3-10* операций, следовательно, для нашего расчета потребуется 10 с или 116 сут. Решение такой задачи обойдется в 140 тыс. руб., если только машина не ошибется за это время и не придется решать задачу снова.

Совершенно очевидно, что обычный путь в данном случае не пригоден. Нужно искать более экономичные пути построения расчетных соотношений и прежде всего избавиться от решения систем алгебраических уравнений. Избежать решения систем можно, если расчетные соотношения построить в виде явных схем, как при расчетах тепловых процессов.

3.4. Равновесие сил

Любой элемент в упругом теле должен находиться в состоянии равновесия, т. е. алгебраическая сумма всех действующих на него сил должна быть равна нулю. Для тел, движущихся с ускорением, в соответствии с принципом Даламбера к внешним силам нужно добавить еще силы инерции.

Внешними по отношению к каждому элементу яв-/1Я0тся силы упругости, действующие со стороны сосед-