них элементов (рис. 3.5), поэтому нужно записать сумму внешних сил и приравнять ее силам инерции. Каждая внешняя сила равна произведению соответствующего напряжения на площадку, по которой напряжение действует. Если элемент имеет размеры /г», hy и Лг, то сумма проекций всех сил на ось х запишется в виде

АЛ К ~ + А - 0-) +>ЛКг - =

где их - ускорение элемента в направлении оси х; т - масса элемента.

Аналогично можно записать проекции сил на две другие оси, но прежде каждое из полученных таким образом уравнений разделим на объем элемента (hxhz):

гу

(3.6)

где p=m/{hxhhz)-плотность материала, из которого сделана конструкция.

Нетрудно заметить, что все три уравнения (3.6) очень похожи. Каждое следующее уравнение можно получить из предыдущего простой заменой индексов: X па у на г, z на х. Такая аналогия говорит о том, что упругие свойства материала во всех направлениях одинаковы или, короче, что среда является изотропной. Мы воспользуемся свойством изотропности, чтобы вместо трех уравнений записать одно. Если в дальнейшем после приведенного уравнения будет напечатано «и т. д.», значит, два других уравнения не приведены, но их можно получить циклической перестановкой индексов.

В уравнениях (3.5) мы не учли сил тяжести. В некоторых областях, например, в строительной механике, эти силы играют большую роль, так как на строительные конструкции часто действует только сила собственного веса. В случае расчета вибраций радиоаппаратуры, когда ускорения в десятки и сотни раз превышают ускорение свободного падения, основными силами являются силы инерции, а вес существенного значения не имеет.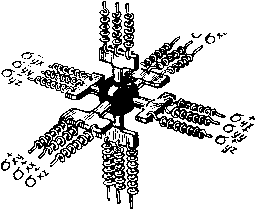

I М I N N

Рис. 3.6.

Если потребуется учет сил biox?

тяжести, то их можно ввести в уравнения равновесия сил.

Проекции ускорения на координатные оси можно выразить через перемещения какой-либо точки элемента. В качестве такой точки разумно взять центр тяжести элемента или его геометрический центр. В этой точке мы и будем помещать узел сетки и определять функции перемещений. Заметим, что точно такие же

уравнения движения (3.6) получатся, если в узлах сетки сосредоточить всю массу элементов и соединить эти массы упругими связями, сила которых равна силам упругости (рис. 3.6). Таким образом, представление сплошного тела в виде отдельных элементов довольно больших размеров и запись для каждого элемента уравнений типа (3.5) равносильны замене этого тела моделью, состоящей из отдельных масс, соединенных пружинами. К сожалению, нарисовать такую картину не просто.

Замену сплошной среды конечным числом сосредоточенных масс называют дискретизацией среды. Разумеется, дискретная среда движется не так, как сплошная, непрерывная. Различие будет тем существенней, чем больше размеры элементов и чем меньше длины волн и частоты колебаний.

Если бесконечно уменьшать размеры элементов, то получится непрерывная среда, для которой и решается задача. Уравнения (3.5) превратятся в дифференциальные уравнения в частных производных

дг

ра и т. д.

Решение таких уравнений, если только его удастся получить, будет точным. Наше же решение будет приближенным вследствие погрешности дискретизации.

Вернемся к выражению проекций ускорения на координатные оси. Ускорение представляет собой приращение скорости. Поэтому вначале определим выражение скоростей через перемещения. Возьмем три момента

17-421 07

времени f-f-T, t и t-т, разделенные равными промежутками т. Обозначим перемещения узла модели в направлении X в эти моменты времени через u{t-\-C), и н u{f~-x). ПрирапЕ,ения перемещений в секунду и соответствует скорости на интервалах ( + т) .. Л и /. .. (t-т):

u{t - i:/2) = - - х)]/т:.

Приращение скорости в секунду на интервале (-1-т/2) ... {t-т/2) будет определять проекцию ускорения на соответствующую ось:

а=[?К-Ьт) -2«4-w(f-t)]/V. (3.7)

Введениал выше система обозначений в разностных формулах, согласно которой величины, отиосяиаиеся к различным узлам сетки и различным моментам времени, имеют индексы, соотостствуюнше номерам узлов и моментов времени, является удобной при программировании задачи для реигення на ЦВМ. В программе организуются счетчики номеров узлов по координатам и времени, имеющие тс же обозначения, что и индексы у величин в формулах, н не цредставляет труда чисто формально перейти от разностных формул к формулам в программе, запнсанггой на одном из алгоритмических языков в машинном коде. Однако в теории упругости используется своя система обозначения величин. Величины напряжений и деформаций снабжаются буквенными индексами, указывающими направление действия напряжений и направления нормалей к площадкам, к которым приложены напряжения [3]. Если к этим индексам добавить еще номера узлов сеткн, то обозначение получится слишком сложным. Поэтому в дальнейшем мы примем другую систему обозначений. Индексы, принятые в теории упругости, сохраним, а индексы, соответствуюш,ие номерам узлов сеткн, заменим обозначениями координат и Бремени в скобках, как это делается при обозначении аргументов функций в математике, Например, нормальные напряжения, действующие в направленнн х и измеренные в узле сетки с координатами л, t}-\-h, Z в момент времени /-f т будут иметь обозначение

<хх{х, y-h, г, -fT).

При этом аргуА!енты х, у. z к i будут принимать дискретные значения, соответствующие координатам

узлов сетки. Такая система не менее удобна, чем примененная выше. Например, прн программировании задачи на алгоритмическом языке фортран разностные формулы будут переписываться без существенных изменений.

Далее, для упрощения обозначений и сокращения занимаемого формулами места среди аргументов в скобках будем сохранять только те, которые отличны от координат центрального узла [х, у, z а I), т. с. будем записывать Oxiy-, i+т). В этих новых обозначениях и записана разностная формула для ускорения (3.7).

Перемещения и можно измерять относительно любой неподвижной точки, поскольку начало отсчета при вы-чпсленщ разностей роли не играет, но его удобней вести от точки, где находился узел в пиложепии равиовесня revia. Однако если тело вдруг начинает двигаться в пространстве как единое целое, продолжая при этом деформироваться, то перемещения отииснгельно первоначального положения могут быть велики, а разности перемещений соседних узлов - незначительны. Чтобы при этом получить достаточную гочиосгь расчета, нужно вычислять перемещения с большим количеством знаков. В этом случае систему координат удобнее сделать подвижной, движущейся вместе с телом, например с центром массы его. Если тело при этом ие испытывает линейных или угловых ускорений, то в расчете ничего не изменится. Если же появляются ускорении, то их можно учесть в виде дополнительных сил в уравнениях (3.6).

3.5. Уравнения движения в перемещениях

Уравнения (3.6) связывают между собой силы и ускорения и являются уравнениями движения элемента. Если бы силы не зависели от перемещений, то проекции ускорений были бы постоянными величинами н элемент двигался равноускоренно. Но при движении элемента внутри упругого тела все происходит гораздо сложнее. Как только возникают напряжения, появляются ускорения ц элементы начинают двигаться. Движение элементов друг относительно друга изменяет величину деформаций и, счедоватсльно, напряжений. Изменение напряжений приводит к изменению ускорений, т. е. скоростей и перемещений. Круг замкнулся. Движение упругого

тeлa н происходит вследствие взаимосвязи перемещений и ускорений. Чтобы разобраться в этой взаимосвязи, 7* 99

Геиштршесний центр /

Цешпр тссы

Рис. 3.7.

нужно в уравнениях (3.6) выразнтр, 1и11[ряжсния через персмсшснпя.

Мы уже знаем, как иыражать перемелцеиия через деформации (см. формулы (3.4) и (3.5)), следовательно, осталось определить деформации через перемещения. Нужно только условиться, в какой точке элемента брать эти перемещения, Ведь сам элемент деформируется и различные его точки движутся по-разному,

Вопрос, казалось бы, простой. Конечно, нужно брать перемещения в центре элемента. Но оказывается, у элемента по крайней мерс два центра - центр массы и геометрический центр. Нел и элемент однороден, т. е. сделан из одного материала, то его геометрически!! центр и центр массы совпадают, а если элемент неоднороден (рис, 3,7), то не совпадают,

С физической точки зрения перемеп1,ения нужно вычислять в центре массы, где сосредоточиваются инерционные силы. Но, к сожалению, .это затрудняет вычисления. Оказывается, что в веодиородных конструкциях, каких S радиоаппаратуре много, центры масс располагаются не на одинаковом расстоянии друг от друга (рис. 3,8). Придется вычислять все 3.8. эти расстояния, множить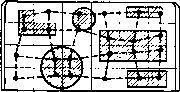

Рис. 3.9.

напряжения на напривляюп!.!!? косинусы п дс.чать много других расчетов.

Л что будет, если вычислжь перемещения и геометрическом центре элемента, а не в центре массы? Очевидно, в расчете иояиягся погрешности, которые будут исчезать в однород,ии> телах. Погрешности сократятся также при уменьтении размеров элементов. Пам придется примириться с этими погрешностями, но при расчетах пеодиородных тел для получения юй же точности расчета нужно брать размеры элемсптов меньшими, чем при расчетах однородных тел. Деформация растяжения есть относительное удлинение, т. с. oTHouieHne прира-пения длины к самой длшш, Г,сли, [шиример, требуется определить деформации удлинения в направлении осп -v между узлами (х--Л) н" к (рнс. 3.9), то сделать это очень просто. Предположим, что узел {x\h) пере-местплея в направлении х на расстояние u{x-\-\i), а узел л;--на расстоящк и. Тогда удлинение этого участка тела составит Ь,1 = и{хЛ-Ь,)-и. Взяв отипшсние этого прпрап,ення длины к первоначальной длине i~hy, получим величину деформации удлинения е+ (K-f ft) - я 3 gj

Теперь ртужно отнести нолучениое удлинение к какой-либо точке участка между узлами х и {x-hx)- Если бы мы растягивали резиновую полосу п других деформаций, кроме гх, не было, то иа всем рассматриваемом участке относительное длнненне бт-Jлo бы одинаковым. Если же процесс деформирования происходит быстро нли, кроме растяжения в направлении х, имеются cnic другие деформации, то деформации zx в разных точках нишесо

737356