
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) ( 10 ) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (10) есть замкнутая более или менее сложная кривая. Обыкновенно изучают кривые, получающиеся в том случае, когда только один из пяти коэффициентов в формулах (11.15) не равен нулю, т. е. изучают в отдельности кривые аберраций, определяемые только одним из коэффициентов. Каждая из пяти аберраций, определяемых одним из коэффициентов в формулах аберраций, имеет особое название. Аберрация, обусловленная коэффициентом А, называется сферической аберрацией; коэффициент В определяет кому, С - кривизну поверхности меридиональных фокусов астигматического элементарного пучка, D - кривизну поверхности сагиттальных фокусе того же пучка, Е - дисторсию (изображения). Необходимо отметить, что в действительности случаи, когда система обладает только одной аберрацией, являются исключительными; обычно системы имеют все пять аберраций. Различные комбинации аберраций для различных точек предмета дают иногда очень сложные кривые распределения точек пересечения лучей, принадлежащих к одной определенной выше совокупности лучей, с плоскостью изображения. Если допустить, что оптическая система не дает аберраций в плоскости выходного зрачка, т. е. что выходной зрачок есть безаберрационное, идеальное изображение входного зрачка, то каждой совокупности лучей, выбираемой указанным способом для исследования распреде.ления лучей по выходе их из системы, в пространстве предметов соответствует пучок лучей, расположенных на конической поверхности с вершиной в изображаемой точке и проходящих через точки окружности в плоскости выходного зрачка с центром на оптической оси. На самом деле, вследствие аберраций в зрачках, окружности в плоскости входного зрачка соответствует замкнутая кривая в плоскости выходного зрачка, отступающая по форме от окружности. Но эти отступления невелики, и ими можно пренебречь при решении всех задач, связанных с качеством изображения, так как этот вопрос по своей природе не требует особо точных ответов. Если распределение лучей в пучке, выходящем из оптической системы, известно, то в некоторой степени можно судить о распределении световой энергии в пятне рассеяния по большей или меньшей плотности точек пересечения лучей с плоскостью изображения при условии равномерного распределения точек пересечения тех же лучей с плоскостью выходного зрачка. Найденное таким образом распределение энергии соответствует действительному только в случаях значительных величин аберраций; у более совершенных систем с хорошим исправлением аберраций распределение световой энергии в пятне рассеяния есть результат интерференции когерентных лучей и потому место наибольшей густоты точек пересечения лучей может не быть местом наибольшей освещенности. I В дальнейшем при исследовании распределения лучей в пучке удем рассматривать совокупности их, определяемые пятью йкружностями в плоскости выходного зрачка с радиусами, длины которых относятся как I : 0,8 : 0,6 : 0,4 : 0,2, т. е. образуют Арифметическую прогрессию. Сферическая аберрация. Если коэффициенты В ~ С - D - Е равны нулю, то оптическая система обладает только сферической аберрацией третьего порядка; координаты точки пересечения луча с плоскостью изображения определяются уравнениями 6g = Am (pi- + М"); bG = AM {m" + M-). (11.16) Переходя к полярным координатам в плоскости выходного зрачка и принимая за полярную ось Оу, имеем m=pcos8; M=psin9, где р и 9 - полярные координаты точки с прямоугольными координатами т, М. Тогда откуда 6g = Лрсозб; bG = Лрзше, 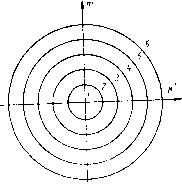 Рис. 11.7 Следовательно, при постоянном значении р кривая, описываемая лучами при их пересечении с плоскостью изображения, является окружностью с радиусом, равным Лр*. При этом из соотношения = ctg 6 вытекает, что каждой точке на выход-йом зрачке соответствует точка в плоскости изображения, распо-Доженная в той же меридиональной плоскости, что и первая точка. "1 Между окружностями с центрами на оси системы в плоскости ♦ыходного зрачка и соответствующими им окружностями в пло-**ости изображения существует подобие особого рода с переменим масштабом подобия, зависящим от радиуса окружности р. .Вномерно нанесенны.1\1 окружностям на выходном зрачке (рис. II.7) соответствуют в плоскости изображения окружности С очень быстро растущими радиусами. При радиусах, численные ения которых меняются по этому закону, в плоскости изобра-ия получаются фигуры, представленные на рис. И.8. В Я. 11. 1 указаны относительные значения р, причем за единицы измерения для обеих величин условно приняты радиусы окружностей с номером 6; числа обоих столбцов не могут быть сравниваемы друг с другом, так как в действительности единица первого столбца имеет размеры радиуса входного зрачка, а единица второго обычно не превышает малых долей миллиметра. Площади последующих зон быстро растут, так как лучи сильно концентрированы в середине; количество их быстро уменьшается к краям изображения. Расчет показывает, что если разделить кружок рассеяния пять частей, отделешинх окружностями, радиусы которых ме- <>!} Таблица ИЛ 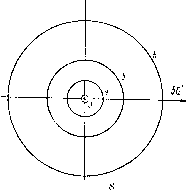 Рис. II.
няются через равные промежутки в пятую часть радиуса зрачка, то в первом кольце (наименьшем) сосредоточивается 34% лучей из числа всех, равномерно заполняющих выходной зрачок, хотя площадь кольца составляет всего 4% всей площади пятна; во втором кольце сосредоточивается 20%, в третьем - 17%, в четвертом-15%, в последнем - 14%. Как уже было указано, вследствие интерференции лучей в системах с умеренными значениями сферической аберрации, действительное сосредоточение световой энергии в центральной части пятна рассеяния значительно превышает то, какое характеризуется приведенными цифрами, полученными без учета дифракционных явлений; правильные результаты дает дифракционная теория изображений (см. гл. X). Если экран, на котором получается изображение точки, перемещать параллельно самому себе вдоль оптической оси, то диаметр кружка рассеяния, получаемого на экране вследствие сферической аберрации, изменяется. Пусть луч КМ (рис. 11.9), соответствующий краю выходного зрачка, пересекает ось в точке М, а параксиальный луч - в точке G, так что GM представляет продольную сферическую аберрацию системы; при смещении плоскости установки по направлению от G к /И до некоторой
Рпс. 11.9 плоскости Р, перпендикулярной оси и проходящей через точку Л, 1аблюдается сначала уменьшение диаметра кружка рассеяния, к потом увеличение его. Плоскость Р называют плоскостью наименьшего кружка рассеяния. В простейшем случае, когда поперечная аберрация может быть представлена единственным членом третьего порядка, а члены высших порядков отсутствуют, плоскость наименьшего кружка рассеяния находится на расстоянии трех четвертей длины GM от гауссовой плоскости; радиус наименьшего кружка рассеяния в четыре раза меньше, чем в гауссовой плоскости. Вывод, выполненный уже Ньютоном, изложим в более обычном для современного читателя виде. Рассматриваемый луч КМ (рис. 11.9), пересекающий ось под углом «, имеет поперечную сферическую аберрацию, измеряемую отрезком GHq в гауссовой плоскости. Согласно первой из формул (11.16), этот отрезок определяется уравнением GHq = 8g = Ат\ Так как величина т пропорциональна углуК то можно написать GHq = аи\ гле а - коэффициент пропорциональности. Из треугольника MGHg имеем 8g = m6s, т. е. 6s = аи. Назовем высоту пересечения луча KiHq с плоскостью РА буквой h, а расстояние плоскости РА от гауссовой плоскости - Шт{т <0); из треугольников МАН и MGHq имеем Диаметр наименьшего кружка 2h определяется положе-рем точки пересечения крайнего луча с каким-то другим, под-Шжащим опре.челению лучом; для первого луча имеем /г« --= - {aui - Аш) Нк, второго fmin = = - (a«min - Am) «min- Исключая h, находим А„ mm к т = а- "mm - Ик :a(Mmin + "min«« + "«)- Минимум значения А,„ при переменном и,„ и заданном и получается, когда " («min + «min«« + III) = 2Mmin + = 0; отсюда находим "mln---2~ • Это значит, что искомый луч образует с осью угол, в два раза меньший, чем краевой, и с обратным знаком. Подставляя вместо его значение через и, получаем-ля При ЭТОМ ft« = - (aul - An,i„) Uk = T. e. четверть поперечной аберрации в плоскости Гаусса. Таким образом, оба положения доказаны. Рассматривая изображение точки, даваемое системой, которая обладает только сферической аберрацией третьего порядка, меняя плоскость установки от гауссовой плоскости в сторону точки М, наблюдают следующую картину: сначала видна яркая точка с большим ореолом, при передвижении плоскости яркость в центре мало меняется, ореол уменьшается, но его яркость растет, становясь сравнилюй с яркостью центра; в плоскости наименьшего сечения яркость фона максимальная, затем начинается быстрое расплывание картины. Отличительная черта сферической аберрации по сравнению с остальными - ее независимость от положения точки-объекта в плоскости предмета. Когда объект на.кодится на оси, все остальные аберрации (в монохроматическом свете) исчезают и остается одна сферическая аберрация. Это свойство относится также и к более общему случаю сферической аберрации всяких порядков. Кома. Кома, определяемая выражениями 6g = Bi(3m"- + Ar)/,; ЬС = 2BimMli, J пропорциональна первой степени удаления точки-предмета от оси и второй степени апертуры. Для изучения комы снова рассмотрим совокупности лучей, определяемых окружностями в плоскости выходного зрачка. Покажем, что каждой окружности в плоскости выходнго зрачка соответствует окружность в плоскости изображения. 66 Переходя, как и раньше, к полярным координатам, получаем б = Bip" (3 cos 9 + sin2 6) = 5ip2/i (2 + cos 20); bG = BiP" (2 cos 9 Sin 0) /i = Bi/ip2 sin 29. Отсюда 8g-2BJiP = 5i/ip4os2e; 6G= fii/ip2sin20. Из этой системы уравнений находим ibg~2BJiP"r -j-bG = (ВЛрТ- (И. 18) Следовательно, точка с координатами bg, bG описывает окружность, радиус которой R = BJg пропорционален квадрату радиуса-вектора р; центр ее, рас- i, положенный в меридиональной плоскости, находится на расстоянии 2fii/]p от гауссова изображения; это расстояние тоже пропорционально квадрату р. Если р меняется по избранному ранее закону арифметической прогрессии, то радиусы окружностей в плоскости изображения растут как квадраты целых чисел, а расстояния между последующими центрами окрул<ностей растут как члены арифметической прогрессии (рис. 11.10). Нужно обратить внимание на то обстоятельство, что когда луч вычерчивает окружность на выходном зрачке, его пересечение с плоскостью Гаусса описывает окружность дважды, вследствие наличия коэффициента 2 в аргументе косинуса И синуса. Если луч двигается радиально в плоскости выходного зрачка, Tv е. величина 9 постоянна, р переменна, то соответствующая точка пересечения луча с плоскостью изображения также движется по прямой. Все эти прямые проходят через гауссово изображение точки. Огибающей всех окружностей служит пара прямых, расположенных под углом 30° к оси симметрии изображения. В самом деле, из уравнения (11.18), полагая для краткости Blp = а, Я{»}учаем дифференцированием по а - 2(6 -2а) -а = 0, 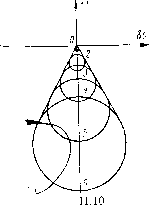 Рис. a = -bg. (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) ( 10 ) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|