идеального положения пропорционально кубу /, так что изображение точки, лежащей близко к оси, очень мало отклонено от своего идеального положения, в то время как изображение удаленной от оси точки отклонено значительно, вследствие чего нарушается подобие между предметом и изображением. Рассмотрим изображение прямой, лежащей в плоскости предмета и не проходящей через оптическую ось некоторой оптической системы, обладающей дисторсией. Изображение этой прямой в случае идеальной оптической системы, обладающей теми же кардинальными точками, что и рассматриваемая система, должно было бы приставляться прямой ВС (рис. 11/14). Так как рассматриваемая нами оптическая система обладает дисторсией, То каждая точка В изображения прямой отклонится по направлению ОВ на некоторую величину равную

Е1, где / - расстояние от оси

до точки, изображение которой совпадает с точкой Вк {к - но-

мер точки).

постоянно и равно линейно-

Пусть ОВк = /; отношение У увеличению системы р. Можно поэтому написать

B.K==-§rl=-~OBhec,o,

TnLVJnZeuTR "пГ" "Р"ВД"«У«РНОЙ к прямой ВС и направлением UB. Полагая для краткости

получим

ВкВ,

а sec (0.

ппетпя" ~ Р"" изображение прямой пространства

S точекТтпйп""" геометрическое место изображений всех точек этой прямой; из сказанного выше следует, что уравнение кривой Во5з в полярных координатах (ОВо - полярная ось, (О - полярный угол) имеет вид

где R 74

Р = i? sec (О + а see со = р sec со (1 -f sec со ) , ОВ,.

Кривая может быть построена по точкам и имеет вид, пред--р-авленный на рис. 11.14, если дисторсия положительна (подушкообразная дисторсия); если дисторсия отрицательна, изображение прямых имеет кривизну, направленную в сторону центра (бочко-эбразная дисторсия). Дисторсия искажает форму контуров, в особенности на краю поля; углы между элементами кривых могут значительно менять свою величину.

Рассмотренными пятью аберрациями исчерпывается перечень аберраций третьего порядка для монохроматического пучка лучей.

Комбинированные аберрации. Аберрации третьего порядка в чистом виде почти никогда не встречаются, за исключением сферической аберрации для точки на оси системы. Обычно имеется комбинация всех пяти аберраций; кроме того, к ним добавляются члены аберраций более высоких степеней разложения, о которых подробно будет сказано ниже. В общем случае, когда ни один из коэффициентов Ai, В, . . ., не равен нулю, распределение энергии в пятне рассеяния зависит от четырех величин и систематическое изучение всевозможных комбинаций коэффициентов содержит непреодолимые трудности.

Если рассматривать только форму кривых аберраций, не интересуясь их абсолютной величиной и положением, можно уменьшить число параметров с пяти до трех. В качестве иллюстраций разнообразия, создаваемого распределением лучей, приводим несколько чертежей, соответствующих различным комбинациям коэффициентов /1 и В (рис. П. 15-11.19).

Полагая в формуле (11.15) = = О и принимая за единицу коэффициент комы Bil, можно написать

Sg = Зт + ЛГ+ Am;

6G = 2тМ + ВМ,

А = Cl; В = Dil\

Сферическая аберрация на рис. 11.15-11.19 во внимание не принята, так как для точек, расположенных далеко от оси, она играет второстепенную роль.

к Для сравнения приведен рис. П.20, изображающий аберра-ронную картину фотографического объектива «Нептун 8» ~210мм, 1 : 4,5) для наклонного пучка, образующего угол 27° Г осью. Число окружностей на входном зрачке здесь доведено iO 16, вместо 10 для предыдущих рисунков; число точек на каждой окружности 32. Объектив «Нептун» обладает большими аберрациями высших порядков, что объясняет сложность аберрационной картины.

Рис. 11.15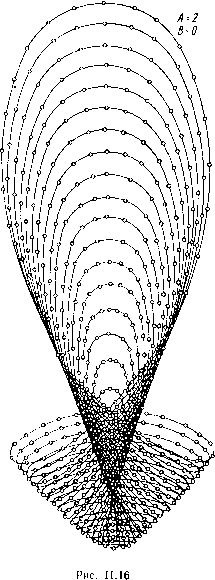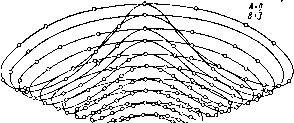

Рис. 11.17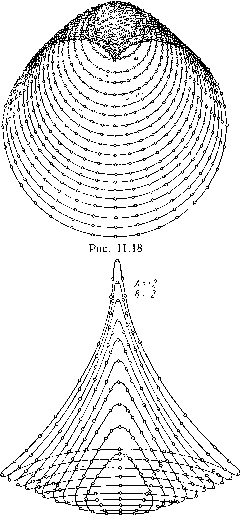

Рис. 11.19

Определение коэффициентов аберраций третьего порядка центрированной оптической системы

Выражения сумм S через коэффициенты Ь. В начале главы было показано, что если обозначить через W угловой эйконал, т. е. оптический путь РММ-М МР (см. рис. II.2) между основаниями перпендикуляров, опущенных на луч из центров О и О плоскостей предмета и изображений, то координаты у и г, у и z точек пересечения луча с этими плоскостями получаются по формулам (II.6) и (II.7)

1 dW

п д\1

1 dW

п dv

= г; -

п dv

f - Су

где р,, V, р, , V - направляющие косинусы луча до и после пре ломления через систему.

Функция Wобладает такими же свойствами относительно координат р, v, ц и v, как и функция относительно т, М, у н Z (см. стр. 59). Поэтому, обозначая через е, е и б выражения г = tx2+.v е = tx2+v б - рр + имеем для Ц7 следующее выра-

жение:

Рис. 11.21

(11.22)

Функция W зависит от положения предмета. Обозначим через Wf значение функций W, когда плоскостью предметов является передняя главная плоскость Я; пусть А и А - расстояния от соответственных главных плоскостей до плоскостей предмета и изображения.

Обозначим через т отношение , обратное угловому увели-чению системы у. Из соотношения h = аА = аА (рис. 11.21) получаем = т. Кроме того, основная формула, связывающая

параксиальные координаты плоскостей предмета и изображения с фокусными расстояниями, имеет вид

-= 1.