
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) ( 18 ) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (18) Но ввиду того, что X = п - пх = "" -= Alzii? = а п. г а. s (« - П) -, имеем Составляем величину А (na8g), обладающую свойством инварианта Лагранжа-Гельмгольца: Обозначим через В выражение перед квадратными скобками: п b (ап - а/г)" тогда A(na6g) = B[...]. (11.73) Покажем, что выражение в квадратных скобках входит как один из сомножителей в коэффициент при величине Р в выражении аберраций третьего порядка для сферической поверхности. Воспользуемся для этого формулами (П.48) и (П.56) для величины rtpCCpbgp и вычислим коэффициент при Р. Он равняется 3 1 , oni-f-jvi ; 2 1 (X, - s,r (x,-s-,y---h,!,fhl J "i Ух- - 3sixl(aiw\- .x\w\ Это выражение легко привести к следующему виду; - А. [sfcoi (со? + Q?) + (Зсо? + Q?) + (П.74) Здесь н далее значок f. . .] означает выражение в квадратных скобках в ире,?,1ду1цей формуле. Принимая во внимание замечания, сделанные на стр. 91 при выводе формулы (11.47), величины sj-, сор Q.x,Xi и w-x в формуле (11.74) можно заменить на s; со; Q; х и ш. После этого легко видеть, что коэффициент при Р в правой части формулы (П.74) совершенно одинаков с коэффициентом при В в правой части формулы (11.73). Другими словами, выражения для сумм Sj, . . ., 5у (11.57) с добавлением членов, зависящих от несферичности поверхностей, имеют вид 5; = 1;/!«(/. +В.); 8п = 1:уЛРк+ Bk)-JWk, 5v = (Pk + B,)~3J /,2 -n (11.75) Из этих формул вытекает следующее важное следствие: величины Вк, зависящие от деформации поверхности, складываются с величиной Рк той же поверхности, и обе величины действуют совместно; ни на W, ни на другие функции от деформация не влияет. При вычислениях сумм Зейделя с учетом деформации по формулам (11.42) и (11.43) нужно к величинам Р добавить соответствующие величины Вк и произвести те же вычисления - умножения на ИТ. д. - с суммой (Рк + Вк), что и с в случае сферической поверхности. Если пользоваться табл. II.2, то следует добавить после столбца Рк еще следующие столбцы: (АаЯк), :(Ап), j, Рк + Вк; дальше никаких изменений по сравнению с таблицей П.2 не будет. Таким образом, выражения поперечных аберраций 6g и 6G для случая асферических поверхностей будут иметь вид - 2n8g = SW (со + У) + Su (Зсо + ) + + (35п1 + /5iv) сода + SW; (11.75*) Примеры применения этих формул будут даны в главе о расчете оптических систем с несферическими поверхностями во второй части книги. Отступление от отношения синусов и кома Предположим, что оптическая система исправлена в отношении сферической аберрации для определенного положения предмета. Точка на оси этого предмета изображается идеально в виде точки. Но всякая точка плоскости предмета, отстоящая от оси на некотором, хотя бы очень малом расстоянии, изображается асти1;ма-тично вследствие комы, и кружок рассеяния, вызываемый комой, растет пропорционально расстоянию точки от оси. Аббе показал, что изображение этих точек оказывается идеальным, если соблюдено условие синусов, т. е. если для любого луча, проходящего в пространстве предмета через точку на оси и через ее изображение, имеет место соотношение = где 7 - угловое увеличение, соответствующее положению предмета и его изображения. Если отношение синусов этих углов не постоянно, то условие синусов не выполнено. Отсюда вытекает, что отступление от закона синусов должно быть связано с комой оптической системы. В некоторых курсах оптики отступление от закона синусов излагается таким образом, что читатели склонны рассматривать его как какую-то особую, шестую аберрацию системы; ее называют иногда даже аберрацией Чеберле. На самом деле отступление от закона синусов представляет собой лишь некий признак, по которому можно судить о коме системы, не проделывая тригонометрического расчета хода лучей, излучаемых точкой, находящейся на некотором расстоянии от оси (единственный способ определения комы, если не считать вычисления коэффициента ц). Отступление от закона синусов дает возможность определить с большой степенью точности кому пучка лучей любого отверстия при достаточно малом расстоянии точки от оси. К решению поставленного вопроса о связи между комой и отступлением от закона синусов можно подойти двояко. Можно на основании теории аберраций третьего порядка найти соотношение между отступлением от закона синусов и коэффициентами Зейделя для первой и второй сумм. Такие выводы имеются, например, в работе А. И. Тудоровского [1 ], а также в первом издании этой книги [2]. Однако больший интерес представляет геометрический вывод, из которого вытекает более общая связь, распространяющаяся на аберрации любого порядка. Здесь будет приведено обобщение формулы Штебле-Лихоцкого, изложенное в работе автора [3]. Введем величину бд, определяемую формулой sm и X sin и (11.76) 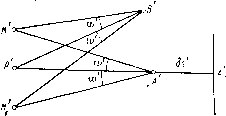 Рис. и..30 где и я и - углы с осью луча, пересекающего выходной зрачок r sin и на расстоянии t от оси; т - предел при ы = О отношения , т. е. величина, обратная угловому увеличению у. Отметим, что величина 65 не равна величине 6sin, приведенной в [2] на стр. 113. Она приблизительно равна ей, но с обратным знаком. Лихоцким было доказано следующее положение. Пусть из точки А, находящейся на оси оптической системы, идутдва симметричных луча, пересекаюш,ихся с осью в точке л, образуя с осью углы со(рис. 11.30); пусть 6s = ЛоЛ -продольная сферическая аберрация этих лучей. Рассмотрим точку В, лежащую на бесконечно малом расстоянии от оси на перпендикуляре коси, проходящем через Л. Два луча исходят из В таким образом, что после преломления они образуют с третьим (главным) лучом РВ те же углы. Поставим условие, чтобы эти три луча Л4В, РВ и М[В пересеклись в общей точке В и фигура М В Mi в точности повторяла фигуру MAmi. Это условие принято после Штебле называть условием изопланатизма: при его выполнении изображение точки В тождественно с изображением точки Л. Штебле и Лихоцкий доказали, что если это условие выполнено, имеет место соотношение 6s + = 0. (11.77) Для доказательства этого положения Лихоцкий делает пред-10жение о том, что точки М и Mi расположены на окружности, роходящей через Р и Л. В реальных оптических системах это едположени, пожалуй, никогда не осуществляется, что в зна-ительной степени лишает его теорему практического интереса. 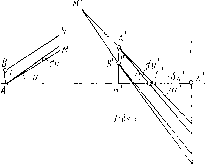 Рис. 11.31 Кроме того, условие Штебле-Лихоцкого не позволяет вычислять значения комы, когда левая часть уравнения (11.77) не равна нулю. Нашей целью является вывод формулы, связывающей поперечную кому меридионального пучка любой апертуры при бесконечно малой величине расстояния предмета от оси с величинами Ь и 6s. Отметим, что при определении комы пучка любого отверстия должны быть приняты предосторожности, совершенно излишние при выводе комы третьего порядка. В частности, необходимо точно условиться о выборе двух крайних лучей, по которым определяется кома. В отличие от Лихоцкого, принимающего в качестве крайних лучей два луча, образующие с главным равные по значению углы, рассмотрим два луча, выбранные таким образом, что синусы углов, образуемых этими лучами с осью, отличаются от синуса угла, образуемого с осью главным лучом, на одинаковые величины. Такой выбор пары лучей люжет быть обоснован следующим образом. Величина плоского потока лучей, исходящего из бесконечно малого источника света, пропорциональна не углу между крайними лучами пучка, а разности синусов этих углов. Таким образом, можно считать, что при выбранной здесь паре крайних лучей энергии обеих частей пучка, разделенных главным лучом, равны. Рассмотрим два бесконечно тонких меридиональных пучка АА1 и BN, исходящих из точки А на оси системы и точки В на расстоянии / от первой (рис. П.31). Расстояние / в дальнейшем будем считать бесконечно малым. Пусть и - угол, образуемый первым пучком с осью. Второй пучок образует такой угол и -j- du с осью, что после преломления он пересекает первый пучок в точке М выходного зрачка. Обозначим через и угол, образуемый пучком AM с осью после преломления. Поперечную кому пучка, соответствующую данной апертуре А п sin и я заданному положению выходного зрачка, определим следующим образом. Вычислим высоту у пересечения с гауссовой плоскостью изображения трех лучей: главного луча, проходящего через центр выходного зрачка Р, образующего угол е с осью, и двух лучей, образующих с осью такие углы и и и , что sin и - е - = 8 - sin = sin о/. Обозначим эти высоты через у, у и у . Образуем величину Km = (11.78) Эту величину назовем комой меридионального пучка для апертуры А. Она, как известно, характеризует степень несимметричности преломленного пучка. Кома третьих порядков не зависит от выбора плоскости установки; это положение неверно для комы пучка большого отверстия, но нетрудно вычислить изменение комы при изменении плоскости установки. Этот вывод будет выполнен ниже; он позволит вычислить кому не в плоскости Гаусса, что вызывает ряд затруднений, а в плоскости АН, содержащей фокусы бесконечно тонких меридиональных пучков MS и МВ, и затем перейти к коме в гауссовой плоскости, которая представляет интерес для конструктора-вычислителя. В плоскости ЛЯ величина / = ЛВ определяется точно по обобщенной формуле Лагранжа-Гельмгольца idcosu du - nl cosm du. (11.79) Определим абсциссу точки Л относительно гауссова изображения Л,, Л. Имеем точки ЛоЯ =AoS + S Н = 6s + S А cos и Рис. 11.32 Но 5 л определяется из элементарного треугольника Л 5 SJ: ALsinu. (11.80) d (6s) Поэтому ЛпЯ 6s sin и cos . Ордината у точки пересечения луча МВ с плоскостью АН равна , лгог I г/ d (6s) . „ , , nl COS и du /тг01\ у =ЛSslnи -г I = I, , smu -\--,--r. (11.81) du « COS и du При составлении выражения для koahj можно заметить, что в выражении для у [формула (11.81)] первый член правой части представляет собой нечетную функцию относительно и и при перемене знака и меняет свой знак, не меняя своего значения. При составлении полусуммы этот член пропадает; вторые Ялены, наоборот, составляют четную функцию от и и при состав- п dl cos и du JJ -дают-;-T-i-r- 4тобы получить в плоско- 2 " rt COS м du - 0 Кении Ьти А , находим сначала значение уг в плоскости Гаусса, соответствующей углу и - О (рис. 11.32). Имеем ndl du yr = dlr = rt du = N/, (П.82) 115 (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) ( 18 ) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|