
 |
| Главная -> Книги (0) (1) ( 2 ) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (2) Длина отрезка ОМ равна 2г sin --. Из треугольника ОМН получаем р = МО cos / МОН; так как /.МОЯ = и---, то р = = MOcos«--= 2г sin-- cos «--Но ц) = и - i, поэтому ы--~ = -~ . Следовательно, аналогично p=2rsin и -f- i P = 2rsin--cos-. Разность p ~p = 2/-sin (I.I5) (1.16) cos cos cos . Ho 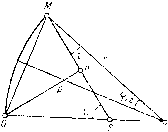 -2Sin ±Ji±i+L Siniiiiiili . Ввиду того, что и - и = г" - i и « Ч- г" = и + г, cos Рис. 1.6 = -2sin-iisini:. Следовательно, -~----Sin (1.17) из фо;:"л (ЙГпГуГм""""" P- Z sin Sin ilzii Bee дальнейшие преобразования имеют целью освободиться от комбинаций углов и + i, i - а + in т. д. и оставить только величины sin i, sin i, sin и и sin и, что позволит обойтись без тригонометрических таблиц. Замечая, что J sin i" - sin i 1 sin и -j- sin 2 TTT И подставляя эти выражения в формулу для р-р, имеем (sin / - sin i) (sin и + sin i) 2 cos -- cos -;r- cos -;r- (1.19) Преобразуем теперь знаменатель, преследуя указанную выше цель. В курсах тригонометрии выводится соотношение 4 cos а cos 6 cos с = cos (а + 6 - с) + cos (а - 6 + с) -f- -)- cos (- а + 6 + с) + cos (а + 6 + с). Применяя его для вырал<ения, стоящего в знаменателе, получаем 4 cos -- cos -2- cos--- 1 + COS (t + t ) + + cos {и - V) + cos (u + 0- Полагая 0 = sin V - Sin i + Sin u; 1 T = cos t" + COS i + cos и j и составляя выраж;ение + - 1, имеем х2.о2 - 1 =2[1 + cos(t + r) + cos(« + t) + cos(« -t)]. (1.21) Таким образом, знаменатель формулы (1.19) для р-р принимает вид (т + - 1) и окончательно (sin / - sin i) (sin и + sin i) (1.20) x3 + o- 1 (1.22) Последняя формула позволяет переходить от р к р. Отметим, что величина р-р всегда мала, порядка продольных аберраций луча. Ее можно вычислять с точностью на два порядка меньшей, чем остальные величины (sin и, sin и, sin i, sin /). Между величинами pus существует зависимость р = ssin«. Величины р и sin i связаны соотношением sin i =sin «--у, которое получается из основной формулы расчета . . г - S . . S sin ы . р 8ШI = -sm и = sin «--= sm «---. г г г Переход к sin и происходит с помощью аналогичной формулы sin и = -у- + sin V = sin V -\--у + Последнюю формулу можно написать и так: sin и = sin « + sin i - sin i + sln« = a + • Переход от поверхности с номером к к поверхности с номером к + 1 выполняется согласно формуле, вытекающей из рис. 1.7: Рк+1 = рк~(1к sin ик- Таким образом, для расчета хода луча имеем последовательность формул: для первой поверхности Pi = sin U{, для любой поверхности 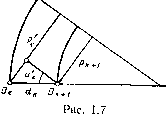 1. sin t = sin н - 2. sin Г = sin i; 3. а = sin « -j- sin i - sin t; 4. T = cosM-l-cosr + cosf; 5 n » л „ (sin - sin 0 (sin и + sin l 6. sinw для перехода (1.23) 7. p„+i = -dsinu. (1.24) Для удобства вычислений необходимо иметь таблицу значений косинусов по данным синусам. Точность в 0,0001 является вполне достаточной при шестизначных вычислениях. Преимущества формул Смита по сравнению с обычными, приведенными выше, следующие. 1. Эти формулы приспособлены для вычислений с помощью счетных машин. 2. Они не требуют применения таблиц, за исключением четырехзначной таблицы перехода от синусов к косинусам. 3. Наиболее ответственная часть вычислений, а именно переход от р к р, требует в большинстве случаев не более четырехзначной точности. 4. Величина р-р пропорциональна поперечной аберрации луча на той поверхности, для которой она вычисляется. Это позво-16 Йяет определить, на каких поверхностях возникают аберрации оптической системы, выяснить их причины и принять меры к их устранению. 5. Вычисления, производимые по формулам Смита, в отличие от вычислений по обычным тригонометрическим формулам не теряют точности при больших радиусах кривизны. Они пригодны и для того предельного случая, когда радиус поверхности делается бесконечным, т. е. поверхность становится плоской, и это свойство формул делает их пригодными для расчета с помощью автоматических машин, так как в данном случае весьма нежелательна необходимость перехода с одних формул на другие при переходе к плоским (или близким к плоским) поверхностям. Главным недостатком формул Смита является их громоздкость, удлиняющая процесс вычисления. Кроме того, могут встретиться такие случаи, когда четырехзначная точность при вычислении разности р-р недостаточна. Это происходит тогда, когда углы i и / имеют противоположные знаки (отражение) или sin и + sin i принимает большое абсолютное значение, что может случиться в системах с большими углами поля зрения или значительными апертурами. В оптических системах, содержащих отражающие поверхности, применение формул Смита требует особых предосторожностей, в частности увеличения числа знаков до пяти или шести при вычислении разности р-р. Тогда четырехзначные таблицы для вычисления косинуса по известному значению синуса должны быть заменены таблицами, содержащими большее число знаков, а может быть, выгодно обойтись без таблиц и вычислить косинус по формуле cos л: = ± "j/ 1 - sin х. 3. РАСЧЕТ ХОДА ЛУЧЕЙ В ПРОСТРАНСТВЕ Расчет хода лучей в пространстве с помощью формул аналитической геометрии Рассмотрим формулы, позволяющие решать задачи, связанные с расчетом хода лучей через оптическую систему более общего !Гипа, чем рассматриваемые до сих пор. Решим сначала такую задачу. Предположим, что известны направление падающего луча, направление нормали и показатели преломления двух сред, ограничивающих преломляющую поверхность. Определим направлениепреломленного луча. Рассмотрим сферический треугольник XNU (рис. 1.8), в кото-fiOM X - точка, соответствующая направлению оси х\ N - точка, соответствующая направлению нормали; U и U - точки, соответствующие направлениям падающего и преломленного лучей. Обозначим через а, Р и у косинусы углов, образуемых направлением и с осями Ох, Оу, Oz; через а, Р и у - направляющие косинусы углов, образуемых направлением U (преломленным г. г Слюсарев лучом); через [.i и - направляющие косинусы нормали к преломляющей поверхности в точке пересечения луча с поверхностью; через Nx - угол между нормалью и осью X. В сферическом треугольнике XNU имеем а = Я cos г -f sin i sin cos / XNU; a X cos i + sin i sin <V I cos XNU. Умножая первое уравнение на -п, второе на п и складывая, получаем па ~ па = (« cost - ncosi) X. (1-25) Положим для краткости « cos Г - п cos i = Л; тогда па -  - па --= ХА. Аналогично яу - пу = vA. (1.25*) Рис. 1.8 2) вычисляется / по формуле Последовательность вычислений такова: 1) вычисляется i по формуле cos; = аЯ + Р!-+ Yv; (1.26) Sim" = 4-sin г, (1.27) (1.28) (1.29) 3) вычисляется Л по формуле А = /). cos i - п cos i; 4) вычисляются а, Р и у по формулам па = па + лА; пР = пр + .11 А; ttV = пу -f vA. Напоминаем, что положительное направление нормали совпадает с положительным направлением распространения света. Формулы (1.29) для луча, лежащего в меридиональной плоскости, принимают вид п sin и - л sin а = А; } (1.29*) п cos« ~ п cos « = А cos ф. Последняя группа формул решает поставленную задачу. Она имеет простое геометрическое толкование. Пусть L - единичный вектор, изображающий падающий луч, проекции которого на оси суть а,р,у; L - вектор, изображающий преломленный луч, с проекциями а, у; N - вектор нормали с проекциями X, [i, v. Группа формул (1.29) может быть заменена одной векториальной формулой ПА =nA + \N. (1.30) Направление вектора совпадает с направлением распространения света. Эта формула удобна в тех случаях, когда направление векторов Л, Л и Л не зависит от положения лучей, например прн вычислении хода лучей через призмы или системы призм. Заметим, что в случае отражения лучей нужно считать п = -п и учесть изменение направления распространения света. Тогда уравнение (1.30) принимает вид А = A~2Ncosi. (1.31) Положительным направлением вектора N считается то, которое совпадает с направлением распространения отраженного света. Приведем одно преобразование выражения А = п cos г" - - п cos i, которое дюжет быть полезно в некоторых случаях. Возведем в квадрат все уравнения (1.29) и сложим. Ввиду ортогональности осей имеем Х + С-+ = I; а- + р2. Y= 1. Кроме того, аа + pfi + yy = cos (Г - t). Принимая во внимание последние соотношения, получаем л2 - 2пп cos (Г - г) + п = (I-.32) Формула (1.30) является основной для метода расчета хода косого луча через систему сферических, а также несферических поверхностей, предложенного И. В. Лебедевым [4]. Пусть а, Рк. Yk и a+i, p+i- Yk+i - направляющие косинусы падающего и преломленного лучей; обозначим через х, Ук, Zk координаты точки пересечения луча с поверхностью к, отнесенные к центру кривизны; пусть - радиус кривизны к-й поверхности. Угол падения i определяется из уравнения cos i = а к+1 Ук Гк •"1 Гк Гк \ ) (0) (1) ( 2 ) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|