
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) ( 24 ) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (24) Можно еще написать Asy в виде Приближенные способы вычисления аберраций пятого и более высоких порядков Сферическая аберрация высших порядков тонких склеенных систем. При расчете оптических систем необходимо учесть влияние аберраций высших порядков. В настоящее время (1963 г.) рядом авторов такие формулы выведены, в частности М. Герц-бергером [8] и Д. Ю. Гальперном в его докторской диссертации. Однако чрезвычайная громоздкость формул для расчета коэффициентов пятого порядка (а тем более коэффициентов более высокого порядка) делает их практически неприменимыми. Кроме того, в тех случаях, когда аберрации пятого порядка велики и должны быть приняты во внимание, то велики и аберрации более высоких порядков; поэтому знание коэффициентов аберраций пятого порядка без знания остальных коэффициентов приносит мало пользы. Прн таких обстоятельствах естественно искать более простые пути расчета приближенных значений коэффициентов аберраций высших порядков. Одна из таких попыток описана в первом издании этой книги [21, стр. 133-140. Здесь приведем без доказательства одну из полученных формул, пригодную для сравнительно простых систем типа двойных склеенных объективов, а именно: А:. „ = -sina; у\ rql -L- - ~i-j , (11.172) где Ase. „ - та доля продольной сферической аберрации, которая вызывается членом пятого порядка; =--j- - нуль- инвариант поверхности к {ар = 1,0). Пример 1. Возьмем объектив из двух склеенных линз со следующими данными: "Tfo 1 = 5; «. = 1,5163; Гз = -2196,0; d, = 2; «3 = 1,6169; F=100; Si = oo; 2 = 4,51. Вычислить сферическую аберрацию для луча с высотой h = = 14,14. Влияние первой и третьей поверхностей незначительно, и им можно пренебречь. Пользуясь формулой (11.172), можно вычислить sm" = 0,000400; /г = 8,015; (7. = 8415; = 11,052; : 0,38. Тригонометрический расчет дает для Asg. „ 0,43. Пример 2. Объектив из двух склеенных линз, значительно переисправленный, с очень большими высшими порядками, имеет следующие данные: Г1 = +31,5; rjlQ2- 1 = 2,0; п., = 1,6169; г; = -135,4; = «3=1,5163; . f = 100; Si = oo; 92 = 7,75. Вычислить высшие порядки аберраций для двух лучей с высотами hi = 10 к hi = 14,1. Как и в предыдущем слчае, влияние первой и последней поверхностей ничтожно. Пользуясь формулой (11.172), вычисляем для ft = 10 sinup = 0,0001; 4 = 11,052; (7=216666; «; = 8,015; для hi = 14,1 isl, п = 0,90; Ase. „ = 3,6. Аберрация третьего порядка равна 0,89 для первого луча и 1,79-для второго. Суммарная аберрация равна соответственно 1,8 и 5,4; точный тригонометрический расчет дает 1,98 и 8,7. В первом издании этой книги [2] при решении приведенных здесь примеров были использованы графики, что дало результаты, более блргзкие к трнгоно-Мет{5ическим, а именно: для первого луча Asg. „ = 1,11; суммарная аберрация 2,00; для второго луча Ase. „ = 6,5; суммарная аберрация 8,3. ? Сферическая аберрация высших порядков систем значительной •Ллины. Одна из основных причин появления аберраций высших порядков (особенно важная в оптических системах с большими )асстояниями между линзами) заключается в том, что вследствие аличия аберраций третьего порядка лучи проходят с большим отклонением от своего идеального пути, определяемого законами гауссовой оптики. Пусть (рис. П.36) ABCD - луч, рассчитанный по правилам параксиальной оптики; ABCD - реальный луч. Вследствие сферической аберрации линзы он направляется по ВС\ пересекает линзу значительно ниже, чем следовало бы, если бы не было аберрации, и после преломления линзой пересекает ось в точке Dj. При вычислении аберраций третьего порядка предполагается, что реальный луч пересекает линзу на расстоянии 1-2,0 от оси; фактически луч пересекает ее в другом месте. Это изменение пути вызывает отклонение луча в дальнейшем его следовании, не принятое в расчет в теории аберраций третьего 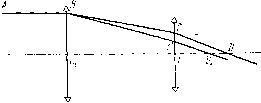 Рис. 11.36 порядка, и последствия этого изменения вызывают аберрации пятого (и более высокого) порядка. Учет таких аберраций представляет большие затруднения. Интерполяционный метод вычисления коэффициентов аберраций высших порядков. Любая аберрация, например сферическая, кома, астигматизм, может быть разложена в ряд по степеням малой величины, принятой в качестве переменной, например величины угла луча с осью, или отношения высоты пересечения луча с входным зрачком к фокусному расстоянию системы, нли (наиболее общий случай) синуса угла с осью луча в пространстве изображения, или угла поля зрения и т. д. Коэффициенты этих разложений определяются на основании значений изучаемой аберрации, полученных из результатов тригонометрического расчета хода лучей через оптическую систему для нескольких значений переменной. Пример. Определим коэффициенты сферической аберрации для объектива. Продольную сферическую аберрацию для объектива можно написать в таком виде: 6s =asinw + 6sin*;/ -fcsinSi. (11.173) В большинстве случаев можно ограничиваться первыми тремя членами разложения. Для определения трех неизвестных коэффициентов а, b п с нужно иметь расчет трех лучей для различных значений и - угла луча с осью после выхода из системы. Если известна первая сумма Зейделя для сферической аберрации третьего порядка, достаточно знать аберрации двух лучей. Пред- положим, что рассчитаны координаты трех лучей, для которых получены значения углов с осью ии и,, щ и аберрации 6;, fis, 0S3. Имеем систему уравнений а sin" «1 + 6 sin«; -f- с sin" «1 = 6si; a sin «2 + 6 sin «2 + с sin* щ = Ы<ь a sin «3 + 6 sin" M3 + с sin Mg = 6S3, (11.174) из которых нетрудно определить коэффициенты а, Ь с Для этого можно подобрать начальные данные и и, для трех лучей таким образом, чтобы отношения sinu sin u„ sin «2 sinful были примерно равны - и - , для чего полагают IlF = -L „ ши, 2 ..... 3 Sin ttg 3 где Их, «2. «3-углы С осью лучей в пространстве предмета. Начертив кривую 6s как функцию от sin и, нетрудно найти графически значения 6s, соответствующие тем и, которые в точности удовлетворяют поставленному условию. Введем вспомогательные выражения А а; В = b sin 3", С = с sin «3-Подставим их в уравнения (11.174): • А sin щ 4--- sin* щ -j-- sinw! = 6sl; sin 1I3 sin «с Sin W., cin sinu sin йо A sm Щ + sin" + - sin*«; = 6s;. sinu. s!n«3 (11.174*) Деля все три уравнения (П. 174*) на siп и полагая, что получаем sin-Mo sin м sinMn = Уз. С = У1, А+±В + -С = у, A + B+C = y,. Решая эту систему относительно А, В и С, находим В = - 7=; 9 27 , 27 „ . 1 9 45 г/з+ 18г/2-- yv 2 " 2 = г/з --у 2 + 9г/1, откуда легко получить Уз- г/2 4 sin* «3 18(/2-2" г/i sm г.ц (11.175) а = г/з --у-а + Эг/!. Необходимость составить интерполяционную формулу для сферической аберрации встречается при оценке качества изображения, например прн исследовании волновой аберрации системы. Примеры такого применения см. в гл. X. Аберрации высшего порядка для точек, не лежащих на оси системы. Значительно большие трудности представляет решение вопроса об оценке качества изображения внеосевой точки. Один из возможных способов исследования опирается на изучение аналитического выражения волновой аберрации для рассматриваемой точки, а для вычисления этого выражения необходимо составить интерполяционную формулу для поперечных отклонений 6g и 6G, учитывая и члены высших порядков. С этой целью пишут выражения для аберраций 6g и 6G в виде разложения в ряд по степеням величин h, Шр и Мр-, вид этого разложения известен из теории аберраций третьего и пятого порядков. При необходимости можно продолжать разложение и дальше, пользуясь тем же методом, но вычисления при этом очень усложняются. Коэффициенты аберраций третьего порядка могут быть вычислены непосредственно по формулам Зейделя. Коэффициенты аберраций пятого порядка могут быть вычислены на основании результатов тригонометрического расчета хода лучей через систему, если предположить, что аберрации точно определяются членами третьего и пятого порядка и что все члены высших порядков в разложении, начиная с седьмого порядка, равны нулю. Так как число коэффициентов пятого порядка равно девяти, то нужно рассчитать ход по крайней мере девяти лучен, в том числе нескольких косых; в действительности необходимо знать аберрации большего числа лучей, чтобы проверить возмож- ность ограничения членами пятого порядка и вообще иметь возможность контроля. Не будем останавливаться более подробно на технике вычисления коэффициентов аберраций высших порядков. Этот вопрос сложен и с принципиальной стороны вследствие того, что сходимость рядов сомнительна, и с практической, так как вычисление большого числа членов - к тому же неопределенного - представляет значительные трудности; кроме того, результаты таких вычислений обычно не представляют особого интереса. Исключением является случай, когда по известным из тригонометрического расчета поперечным аберрациям требуется найти волновые аберрации, чтобы на основании дифракционной теории изображения вычислить распределение энергии в картине изображения объекта. В этом случае, по-видимому, более эффективны графические методы [9, 10]. Сложение аберраций При расчете оптических систем часто представляется целесообразным разделить систему на две или больше частей и изучить их в отдельности. Число свободных параметров в каждой части меньше, чем во всей системе, и исследование всех частей в отдельности может быть выполнено с гораздо меньшей затратой труда и времени, чем исследование всей системы в целом. Однако остается еще решить задачу наилучшего подбора каждой части таким образом, чтобы аберрации всей системы получили надлежащие значения. Для этого нужно уметь «складывать аберрации», т. е. вычислить аберрацию всей системы, зная аберрации каждого компонента в отдельности. В теории аберраций третьего порядка доказывается, что поперечные аберрации, вызываемые каждой поверхностью, с помощью закона Лагранжа-Гельмгольца могут быть спроектированы в любую плоскость изображений и сложены. Это свойство может быть перенесено на аберрации более высокого порядка. В первом приближении можно считать, что поперечные аберрации, умноженные на па (т. е. в сущности превращенные в разности оптических путей), складываются. При более точных вычислениях следует ввести поправки. Общего правила для вычисления поправок нельзя указать. Вид поправки зависит от способа, й помощью которого аберрации получены. Укажем несколько зфдрмул, выведенных Д. Ю. Гальперном [11, 12], позволяющих Й)ешать ряд задач и среди них задачу сложения аберраций. Из эйконала Шварцшильда [13] легко выводится формула 1" sin и \ dbg dyo sm u + sin u (11.176) (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) ( 24 ) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|