
 |
| Главная -> Книги (0) (1) (2) ( 3 ) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (3) Преобразуем выражение А =.« cos i - п cos / Ввиду того, что получаем п cos i = Уп- - п + пЧоъ1, A = Yn- - nj „2 cos2 i „ COS(1.32*) Зная A, можно определить p,,, y, no формуле (1.29): л - ГУ 4- Д г«: (1.34) Теперь известны положение и направление преломленного луча, поскольку известны координаты х, у, точки луча и его направляющие косинусы. Остается осуществить переход к следующей преломляющей поверхности; он производится следующим образом. Пишем уравнение преломленного луча Х - Хк Y -ук Z-zk ««+1 Рк+1 7к+1 где t - величина, зависящая от положения рассматриваемой точки на прямой. Ищем точку пересечения этого луча с поверх- ностью /с+1, радиус кривизны которой равен г. Пусть А = (1.35) , - - расстояние между центрами С и С обеих поверхностей. "+1 Обозначим через дг,,„ у,, .. координаты точки пересечения луча с поверхностью к + 1, отнесенные к новому центру кривизны. Переход от старой системы координат к новой осуществляется по формулам (1.36) Уравнение сферы с номером к + 1 в новых координатах имеет Уравнение луча может быть переписано в виде Х„ = х + ai; К« = у« + f.+if; Z« = z« + у Подставляя эти значения для Х, Уя в предыдущее урав-рие и принимая во внимание переход от новой системы к старой, элучаем (х« - Л« + a.,4f + {у, + ,4f + (2« + tf = г\ к+1- Произведя возведение в квадрат соответствующих величин и помня, что ««+1 + Рк+1 + Vk+1 = 1; Хк + P«+if/« + Y«+i2k = r«+i COS получаем для определения значения 4, соответствующего точке пересечения луча с поверхностью к+1, уравнение tl + 2t (r„+icos i - Л A+i) + rl - r«+i - 2Лл + Al - 0. (1.37) Решив это уравнение относительно t, выбираем то значение корня, которое соответствует первой точке пересечения луча со сферой. Определив 4, имеем K-i-x - ~\ K+iK Ук-х ~ Ук Pk+ii Zk+i = 2к + Ук+1к- (1.38) Как легко видеть, представляет собой «косую толщину» d, т. е. расстояние между поверхностями /с и (к + 1), отсчитываемое вдоль луча. Зная координаты х, точки пересечения луча с поверхностью к + 1 и направляющие косинусы падающего луча Ok+i, Рк+1 и можно по приведенным выше формулам продолжать расчет хода луча через вторую поверхность. Подробности вычисления и схему см. в статье И. В. Лебедева [4]. Вычисления выполняются на арифмометре и не требуют применения тригонометрических величин; кроме того, метод может быть обобщен на случай несферических поверхностей, как это указано в статье [4]. К достоинствам аналитического метода можно отнести следующие: 1) отпадение надобности в таблицах; 2) незначительное количество случаев потери точности (к таким относится случай больших радиусов, при которых определение величины t становится неточным, так как в коэффициентах уравнения, определяющего t, появляются разности больших и близких величин); 3) выполнение вычислений по однотипным формулам, что облегчает процесс вычисления и уменьшает возможности ошибок; 4) наличие контрольных формул, например 4 + (3 + 7.= 1. К недостаткам этого метода следует отнести: 1) полное отсутствие углов в схеме, из-за чего трудно по вычислениям хода луча определить те места в системе, в которых появляются аберрации высших порядков; 2) слишком большое различие между аналитической схемой и обычной тригонометрической, вследствие чего сравнение хода лучей в обоих случаях с первого взгляда невозможно. Впрочем, за отсутствием опыта по применению аналитического метода невозможно дать о нем достаточно обоснованный отзыв; было бы полезно в одном из вновь организуемых вычислительных отделов подвергнуть этот метод подробному исследованию. Расчет косого луча через отражающую поверхность второго порядка Предположим, что в оптической системе одна отражающая поверхность имеет форму гиперболоида или эллипсоида с эксцентриситетом е. Пусть а, р и 7 - направляющие косинусы падающего луча. Они равны: а = cos б cos е; Р = -cos б sine; у = sinS, (1.39) где сферические координаты б и £ известны из расчета косого луча, доведенного до несферической поверхности. Пишем уравнение этого луча в виде X = s+at; Y = l + р/; (1.40) Z = yt, где / - расстояние по лучу от точки М пересечения луча с несферической поверхностью до точки В пересечения луча с меридиональной плоскостью; s - абсцисса точки В относительно вершины отражающей поверхности. Уравнение поверхности второго порядка, отнесенное к вершине, имеет вид f{X, Y, Z) = (e2-1)Х2 + 2гХ -F2 -Z2 = 0. (1.41) Помня, что направляющие косинусы нормали X, [i, v пропорциональны частным производным . > получаем (1.42) где = y7+I7x+M=W- Подставляя выражения для X, У и Z в уравнение поверхности второго порядка, получаем для t уравнение второй степени (а%2 i)p2t[ra + sa (e - 1) - ф] + 2rs + (e2 i)s2 /20. Полагаем для краткости А=ае-\; В = ra-f sa(e-1) -/Р; C = 2rs + (e2- l)s2 -Р; Если > О, полагаем ~ = sin Т, откуда (1.43) (1.44) Если <0, полагаем - = g Т, откуда = i-sin-f seer. Зная t, можно вычислить X, Y и Z по формулам (1.40) и, подставив в формулы (1.42), получить Я, р и v. Угол луча с нормалью i вычисляется по формуле cos i = аХ-}- P.i -f yv. (1.45) Направляющие косинусы а, р и у вычисляются по формулам а = а -2Xcost; р= р -2(xcos/; (1.46) у = у - 2vcos J. Координаты луча, падающего на поверхность, следующую после асферической, определяются из выражений sin6 = Y; s=X--Z, (1.47) после вычисления которых можно продолжать расчет хода луча через следующие за поверхностью второго порядка сферические поверхности по обычным формулам. Формулы Федера Для расчетов с помощью электронно-вычислительных машин очень удобны формулы, предложенные Федером [5]. Луч в схеме Федера определяется с помощью следующих векторов (рис. 1.9): Q {X; Y; Z) - единичный вектор вдоль луча до преломления; Ql (и Уй Zi) - то же после преломления; Т {х; у; z) - вектор, соединяющий вершину поверхности / с точкой пересечения луча с этой поверхностью; 71 (Xi, Ух, Zj) - то же для поверхности 2. Расчет хода луча через сферическую поверхность. Приводим формулы Федера для случая сферических поверхностей. Обозначим через = -; 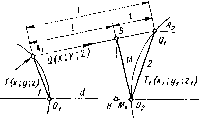 Рис. 1.9 = - кривизны сферических поверхностей 1 и 2; через В - пересечение падающего луча с перпендикуляром М к нему, опущенным из точки Оз; через и Л 2 - точки пересечения луча с поверхностями / и 2; через Х - расстояние Л1Л2 (рис. 1.9). Отрезок I = AiB определяется формулой l = dX - (xX +у¥ + zZ). Проекция на оптическую ось перпендикуляра М определяется по формуле Mx+lX - d. Длина отрезка М определяется следующим образом: М = Ml + Ml + Ml = {х + IX-df + [y + lYf + {z+ IZf = x + y + z + P + 2l (xX + yY + zZ - dX) - 2dx + d» =r = d + x + y + z+l - 2P - 2dx. Окончательно M = x- + y + zP - 2dx + d\ Определим точку пересечения луча с поверхностью 2. Уравнение ее, отнесенное к вершине О, следующее: xi + y\ + zi - 2r2Xi = 0. Уравнение луча Xi - Mx У1 - Му Zi - Mz X ~ Y Z ~ > откуда Xi = Mx + tX; y=-.M,j + tY; = + tZ. Подставляя эти выражения для х, j/j и 2 в уравнение сферы и ХМ + YMy + ZM, = О, помня, что получаем - 2г1Х + М - 2гМ, = 0; (знак + относится ко второму пересечению с поверхностью 2 и обычно не представляет интереса). Вычислим косинус угла падения /: - X = Гг 2 2 {М + tX)X + (My + tY)Y + {M, + tZ)Z МХ + MyY +M,Z + t t -. ~ 2 вычислим величину 1 + - 2r.,/Wx r,X+YriX-M + 2rM, с,Мз - 2Мх = 1 + сМ - 2Мх X + cos i , де С2 = (0) (1) (2) ( 3 ) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|