
 |
| Главная -> Книги (0) (1) (2) (3) ( 4 ) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (4) Зная £, легко получить х, t/j и г: Xi=x + Lx~ d; гг = г + LZ. Остается вычислить направляюшир ifr,rHu„, „ луча У,, Угол опрляТя%Гего™и„ТГу- =[-Ш(1-созЧ)] Косинусы преломленных лучей гнячяим зГ, У-с„„е«„« форм,. (Г;р™Г/„Г?ГГ -Та ni = пХ + (п cos / - п cos о cos {NX); nY = nY + (n cos i - n cos г) cos (TVF); «Zi =. «z (Л cos r - n cos 0 cos (NZ), где - направление нормали в точке преломления. cos(yvX) = = 1 cos {NZ) = - Il „ - где . Сз = - Обозначая через g выражение cos /; --1 cos получаем ДлясГрГчсг™ формул Федера 1. / = dX-(xX + i/F + Z}; 3. Л = + / + г /2 2х + 2. 4. cos г = /х - " X + COS/ 6. Xi = х+ LX - d; 7. y,=y + LY; 8. Zi = z + LZ; 9. cos tl = (l-cosh) \0, g = cosh--rCOSiV. 11. X, = -X + gr(l-c); 12. Y,=Y-gc{, 13. Zl = -Z -gCaZi. Преимущества формул Федера по сравнению с приведенными в первом издании этой книги формулами Кербера для косых лучей заключаются в следующем: 1) полное отсутствие тригонометрических функций; 2) минимальное число квадратных корней (один на поверхность); 3) отсутствие переменных, обращающихся в бесконечность (такими величинами являются, например, s и s в формулах расчета хода лучей, приведенных в начале этой главы). Величина L может, правда, обратиться в бесконечность, если X + cos i = О, но в этом случае луч касается преломляющей поверхности и не участвует в образовании изображения; 4) отсутствие формул, приводящих к потере точности. В частности, случай больших радиусов, который при обычной схеме приводит к потере точности и вызывает необходимость применения новых схем (что для работы с помощью электронной машины является нежелательным), здесь не вызывает никаких затруднений; плоские поверхности не требуют применения специальной схемы. Расчет хода луча через поверхность второго порядка. Формулы Федера могут быть распространены на случай поверхностей второго порядка. Предположим, что поверхность ОА является поверхностью второго порядка. Ее уравнение, отнесенное к вершине О, имеет вид F {х,у,гг) = х1 + y\ + zi~2rx-eh\ = 0. Уравнение луча сохраняет прежний вид: Xt = tX; у = Му+ tY; z = M,+ tZ. Величина t определяется формулой \-ёХ-----• X{cemx+\)jCl где с = Q==KЧcVM + 2cM..-cW(l-eX). Величина L определяется из уравнения L = / + /. Отсюда следуют выражения для х-, f/i", jCj = X + LX - d; Zi = z + LI. (1.48) Определяем cos t = + Гц + Zv гяе ,< л, dF dF Qp дх rD дг rD > 1 P-kx r dp 2 дх 3f дх Тогда cos i - -. Формулу для cos i получаем по-прежнему: -(-У(1~соз0] cosf Положим 28 g = cosi - -cosi, росле чего выражения для Х, Yi, Zi принимают вид
ckxi - 1 D По-прежнему можно пользоваться для контроля формулами X\ + Y\ + Z\ = \; (ckx-~\f + {cyf + {czf = D\ Составим сводку необходимых для вычислений формул Федера для поверхностей второго порядка: 1. l = {d - x)X - yY - zZ\ 2. Mx = x + lX-d; 3. M{x - df-\-y + z - P\ 4. Q = ух + cVmI л- 2cM, - cM (l - ехУ, к г / I X х I -Г x(ceMx-i-\)+Q. 6. = jc -d+ LX; 7. У1 = у + LY; 8. Zi = z + LZ; 9. D = АГТЛЧ?ТТ); 10. cos/ = --; 11. cost= [l - (-(1 - cosO \2. g = cost --j cost; 13. X, = -fX-i; 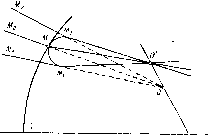 4. бесконечно тонкие астигматические пучки Определения Рассмотрим бесконечно тонкий пучок лучей, ограничиваемый поверхностью конуса с вершиной в точке О. Этот так называемый элементарный гомоцентрический пучок после прохождения через оптическую систему, вообще говоря, перестает быть гомоцентрическим; по выходе из системы пучок имеет особое «астигматическое» строение. Все лучи пучка стягиваются в две линии (фокальные линии) бесконечно малой длины, расположенные во взаимно перпендикулярных плоскостях. В пределе две фокальные линии обращаются в точки и называются фокусами пучка. Предположим, как всегда, что оптическая система имеет ось симметрии. Если центральный луч элементарного пучка (его принято называть главным лучом) находится в меридиональной плоскости,то из теории астигматических пучков известно, что одна из фокальных линий, а именно та, которая образуется сагиттальными лучами, т. е. лучами, лежащими в плоскости, перпендикулярной меридиональной, лежит в этой последней плоскости; ее пересечение с rлaвньfм лучом называется сагиттальным фокусом. Вторая фокальная линия, образуемая меридиональными лучами, т. е. лучами, лежащими в меридиональной плоскости, перпендикулярна последней; точка пересечения ее с главным лучом называется меридиона.1ьным фокусом. Положение сагиттального фокуса вычисляется согласно данному определению, которое можно сформулировать несколько иначе. Рассмотрим точку пересечения двух лучей, исходящих из вершины пучка О и симметрично расположенных относительно меридиональной плоскости. Когда эти два луча беспредельно приближаются друг к другу, точка пересечения стремится к некоторому предельному положению: это - положение сагиттального фокуса, сопряженного с точкой О. Отсюда вытекает возможность определять координаты этого фокуса в случае одной преломляющей поверхности. Пусть МоМО -главный луч падающего сагиттального пучка MiOM, С - центр преломляющей поверхности; СОО - прямая, соединяющая центр с вершиной О пучка (рис. 1.10). Рис. 1.10 Более подробное .зложсние сы. в курсах геометрической оптики, МlOM2, получен вращением главного луча (в ту и в другую у) вокруг оси СО на бесконечно малый угол. Рассмотрим жйок после его преломления через поверхность SM. Главный луч Снимает положение МО, крайние лучи пучка - положение МО и- M-iO; эти лучи должны пересекаться в точке пересечения О главного луча с прямой СО, так как преломленный пучок, в свою очередь, получается в результате вращения преломленного главного луча МО вокруг оси СО. Таким образом, фокус бесконечно тонкого сагиттального пучка находится в точке пересечения главного луча с прямой, соединяющей центр преломляющей поверхности с вершиной пучка. Если поверхность SM несферическая, но симметричная относительно оси SC, то вместо центра кривизны С нужно брать точку пересечения нормали к точке М с оптической осью. Фокус меридионального пучка определяется также в результате перехода к пределу. Рассмотрим два луча, нсходя1их из вершины пучка О и лежащих в меридиональной плоскоси. После преломления эти два луча пересекаются в некоторой точке О, положение которой зависит от угла, образованного двумя лучами в точке О. Когда этот угол беспредельно уменьшается, точка О стремится к некоторому положению, которое является положением меридионального фокуса. Формулы Аббе-Юнга для определения положения астигматических фокусов Случай одной преломляющей поверхности. По Аббе поюление фокусов, как сагиттального, так и меридионального, бесконечно тонких пучков, а также и положение источника света (вершины пучка) определяются их расстояниями от точки пересечения главного луча с поверхностью. Пусть SA (рис. 1.11) - сечение поверхности меридиональной плоскостью; АВ - главный луч; М - верщина падающего пучка; ЛВ - луч, образующий в главным лучом угол du И проходящий через точку СВ - перпендикуляр, - „ «лущенный из центра С на " «туч АВ; длину СВ обозначим буквой q, расстояние ВВ - Приращение величины q - через dq. При /"льнейших выводах «УДем считать величины du, dq и остальные приращения 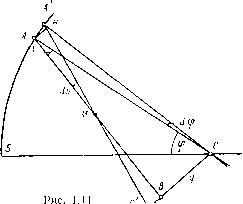 (0) (1) (2) (3) ( 4 ) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|