
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) ( 41 ) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (41) применяя эти формулы для хроматической разности увеличений, получаем 7 =7-11 Ф- (HI.12) где суммирование распространяется на все элементы системы. Напомним, что / = nal имеет ту же размерность, что hiyfi. Для вычислений удобно принимать ар = \; у- = (т. е. = 1); hi = sa. Тогда / = ai (xi - Si) = (xp - sp) Pp. Молено, введя величину т = , написать Lp-Lc (111.13) при этом hi = SiT; yi = Xj; «р = 1. Если предмет на бесконечности (т = 0; «р = 1; /ij = / = - 1), получаем (111.14) Величина С; в простейших компонентах Рассмотрим два случая. 1. Бесконечно тонкая простая линза. Как было показано выше, в бесконечно тонкой линзе 2. Бесконечно тонкая двухлинзовая склеенная система. Рассмотрим общий случай, когда «1 =j= 0. Фокусное расстояние Ф и высоту h принимаем равными единице. Тогда hФ = а~ ai = \. Вычислим С = - (--f-Si.) при Ф1 + Ф2 = 1- Имеем Ф1 = («2 - 1) (Pi - Рг); Ф2 = 1 - Фх- П.-П1 Р2 = "2- 1 Пдаз - ааПа "з - «2 После подстановки ("8 - 1) -0з"з ("а - О „ . \ V2 У 1 V Vl V2 У а2«2 («3 - 1) - аз"з ("г - 1) "а - «2 - а. \ Vl V2 У V2 «4- «1 (л-! Га \ V2 Vl (111.15) Если не делать предположения о том, что а - «1 = 1, то для С получаем следуюшее выражение: (111.15*) «3% ("а - 1) - «а"а ("з - 1 "з - "а В часто встречающемся случае, когда «1 = О и «4 = 1, получаем ДЗ"3 ("а - 1) - "22 ("з - "•3 - «2 3. ТЕОРИЯ ОСНОВНЫХ ПАРАМЕТРОВ Из фор1\1ул (111.7) вытекает, что коэффициенты 5 всех пяти аберраций третьего порядка монохроматического луча для системы из бесконечно тонких компонентов могут быть написаны в таком виде: S = S (m,P, + n-rWi + р,я, + qi\ (111. 16) причем коэффициенты tui, tii, pi, qi зависят только от yi, hi, Ф, т. е. от величин, связанных исключительно с внешними элементами системы - фокусными расстояниями отдельных компонентов, от их взаимного расположения, от положения плоскости объекта и входного зрачка. Действительно, если все перечисленные элементы даны, то можно рассчитать ход обоих вспомогательных лучей на основании формул гауссовой оптики (подробнее см. гл. V) и получить последовательно все hi и г/,-. Существует категория оптических систем, к которым, в частности, относится большинство телескопических систем, для которых величины hi и у1 могут быть заранее определены (например, из требований габарита). В этом случае они непригодны в качестве переменных, с помощью которых можно исправлять аберрации, и поэтому по характеру своему они совершенно отличны от величин Pi, Wi. Последние являются функциями а и /г, т. е. углов первого вспомогательного луча с осью и показателей преломления всех сред компонента. В свою очередь, величины а зависят от раДусов кривизны системыЬт ее показателей и от положения точки пересечения вспомогательного луча с осью, как это видно из рекуррентных формул, определяющих последовательно все значения а: Щ+1 - Щ (III.17) Величины = зависят только от радиусов кривизны и показателей преломления. Таким образом, величины Pi, Wi зависят от «внутренних» конструктивных элементов системы - радиусов кривизны поверхностей и показателей преломления - и еще от положения точки пересечения первого вспомогательного луча с осью оптической системы до преломления через компонент. Последняя зависимость значительно затрудняет систематическое изучение свойств бесконечно тонких компонентов, так как она вводит еще одну лишнюю переменную, также влияющую на свойства указанных величин. Однако можно исключить последнюю переменную и получить величины Pi, Wi в виде функций следующего вида /э = гР + sW + Ы; W= +sW + rjt, (III.18) где Р, W и Jt зависят только от внутренних элементов, а г, s, t зависят от положения точки пересечения с осью первого вспомогательного луча. Такой процесс разделения параметров, входящих в выражение для аберраций третьего порядка оптической системы, с одной стороны, на параметры, зависящие только от внешних элементов, и, с другой стороны, на параметры, зависящие только от внутренних элементов, возможен только в системах из бесконечно тонких компонентов и в высокой степени уп-рощает расчеты. Это вытекает из формул, данных в гл. 11 (см. стр. 83), связывающих значения коэффициентов аберраций третьего порядка с положением предмета. Для бесконечно тонких компонентов зависимости величин Р и 1 от положения предмета могут быть получены непосредственно гораздо проще, чем в результате применения формул гл. 11 для частного случая, когда толщины обращаются в нуль. Приводим здесь вывод этих формул. 1 г. г. С л ю с а р е в. Труды ГОИ, Т. 8. Вып. 76, 1932. Основные параметры бесконечно тонкого компонента 1 v=l v=s v=l " • \ Aan Jt = 7 --> (Ш.19) где суммирование распространяется на все s поверхностей компонента ; так как плоскость предмета на бесконечности, а = 0; по условию as = 1. Высоту падения луча на компонент примем за единицу, если фокусное расстояние системы положительное, и за -1, если оно отрицательное. Параксиальный луч AM (рис. 111.1), проходящий параллельно оси на высоте h, после преломления пересекает ось в точке F. Рассмотрим другой параксиальный луч AMF, пересекающий компонент в той же точке М. Он пересекает ось в точке S до преломления и в точке Fi после преломления. Если угол MFO принят Задача преобразования выражений Р я W к виду (111.18) может быть решена следующим образом. Рассмотрим частный случай, когда бесконечно тонкий компонент изображает предмет, находящийся на бесконечности. Вычислим первую сумму Р и вторую W, приняв величину as, где S - номер последней поверхности компонента, за единицу. Далее вычислим выражения Р я W в общем случае, когда плоскость изображаемого предмета находится на конечном расстоянии. Заметим, что величины а для второго случая связаны линейно с величинами а, соответствующими перг.ому случаю. Чтобы различить углы а в обоих случаях, условимся обозначать величины а, соответствующие бесконечно большому удалению предмета, той же буквой а, но с черточкой наверху. Выражения Р я W являются однородными функциями третьей и второй степени относительно переменных а. Но и выражения Р, W и Jt являются также однородными полиномами относительно переменных а соответственно третьей, второй и первой степени. Поэтому должно существовать соотношение видя (111.18). Определим теперь коэффициенты г, s, t, s и t. Имеем исходные полиномы за единицу и угол AiMA обозначен буквой а, то угол MFiO равен 1 + «1. -J Определим положение плоскости предмета отношением : OS l + ai Ofi ~" «1 которое обозначим через -. 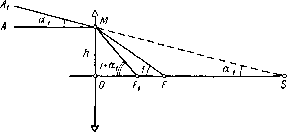 Тогда получим Рис. III.1 (1П.20): где «8 - угол, образованный лучом с осью после преломления; «8 - «1 == 1. Вычислим теперь Р r.W. Если выразить величину радиуса поверхности с номером v двумя способами через а и а, придем к соотношению v+lv+l " - Oty.,.jnv+i CCyy Таким образом, разность ап - аПу является инвариантом, сохраняющим свою величину для данной пары лучей при всех значениях v. Для первой поверхности v = 1 и «1 = 0; поэтому для поверхности с номером к можно написать (III.21) Выражение для Р и W составляются из множителей: И f-\ "«+1 После подстановки вместо и «к. их выражений через а», и а». получаем «к «+1 + «к \ "«+1 (III.22) Если эти выражения подставим в формулы для Р и IF, произведем все выкладки и сокращения, введя, где это окажется возможным, величины Р и W, заменим п- его значением, равньда 1, и «1-его выражением , то получиМ 1 -е (W) 1 =W-f- (4W - 1) + (2 +Я). -(3 + 2я); (III.23) Индекс 1 -е означает, что величины Р и IF вычислены при значении «8 равном -у~£ • Формулы (II 1.23) выведены в предположении, что луч AMS преломляйтся сложной линзой с номером I в точке М на той же высоте/что и луч AM. Проведем через точки 5 и Pj параксиальный преломляющийся через компонент с номером 1 не в М, а в какой-нибудь другой точке и являющийся первым вспомогательным параксиальным лучом системы. Обозначим буквами а и а углы этого параксиального луча с осью до и после преломления у исследуемого компонента. Очевидно, что «1 Заменяя е в формулах (III.23) его выражением через а и а, получаем для (Р) i и (IF) i ()-J- = Р + (4W - 1) + (3 + 2п); (IF) 1 =W+- (2 + Jt). (III.24) Чтобы получить значения величин Р и IFj, соответствующие параксиальному лучу, для которого а равно а, нужно умножить полученные выражения соответственно на а (1 - е) и на а (1 - 8)2 или, что то же самое, на (а - а)* и (а - ау. Это (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) ( 41 ) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|