
 |
| Главная -> Книги (0) (1) (2) (3) (4) ( 5 ) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (5) бесконечно малыми величийами первого порядка; их квадратами и взаимными произведениями будем пренебрегать. Дифференциал дуги А А между двумя лучами АВ и АВ равен гйф, где ф - угол нормали с осью. Опуская из точки А перпендикуляр ЛЯ на луч АВ, в бесконечно малом прямоугольном треугольнике AHA имеем АН = АА cos t, так как угол между касательной к кругу 5Л в точке Л и перпендикуляром к лучу АВ равен углу i. Обозначим через „ расстояние ЛМ по лучу от поверхности до вершины М пучка. Подобие треугольников МАН и МВВ дает , АН ВВ ВВ АВ - AM г d(p cos t dq tm ~ rcosi - tn Ho q = r sin i и dq = r cos idi, и формула (1.49) принимает вид г cos i г cos t di tm ~ rcosi - t„ (1.49) (1.50) Точно такую же формулу можно написать для преломленных лучей: rd(fc(i rcosidi rcosi -1„ (1.50*) где - расстояние фокуса меридионального пучка преломленных лучей от поверхности; Г - угол преломления. Дифференцируя равенство п sin i = п sin г", выражающее закон преломления, получаем ncos t dt = ftjCOS Г di. (1-51) Деля уравнение (1.50*) на (1.50) и принимая во внимание (1.51), получаем после простых преобразований формулу Аббе для бесконечно тонкого меридионального пучка, а именно: п cos i п cos I п cos I - n cos I (1.52) Формула (1.52) связывает величины и t через углы преломления t и t". Для сагиттального пучка соотношения между расстоянием tg от точки пересечения Л главного луча с преломляющей поверхностью до вершины М пучка и расстоянием от той же точки Л до фокуса М бесконечно тонкого сагиттального пучка после преломления могутбыть получены следующим образом. ть (рис. 1.12) AS - падающий луч; AS - преломленный шШ и Ж - сагиттальные фокусы до и после преломления; шшЖАСО обозначим буквой ij). Как было доказано, точки М, м Унтр с преломляющей сферы находятся на одной прямой. Из треугольника АМС имеем sin i sin ii Аналогично из треугольника АМС находим sin t sin гз Умножая первое уравнение на л simj) и второе на п sin i) и принимая во внимание закон преломления, получаем формулу МС ,МС п-= - п :„.(1.53) 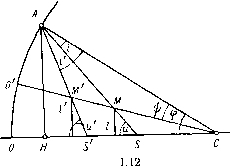 Рис. С другой стороны, проектируя МС и МС на радиус АС, получаем MCcosij) = г - sCosi; MCcosij) = r - tsCosi. I (Ь54) Подставляя в уравнение (1.53) значения МС и МС из (1.54) и деля на cos получаем после простого преобразования фор-, мулу Аббе для бесконечно тонкого сагиттального пучка п п пcos t - ncost n 77 --r-• - Формулы (1.52)и(1.55) решают поставленную задачу в случае одной преломляющей поверхности. Когда преломляющая поверхность плоская, формулы (1.52) и (1.55) принимают особенно простой вид, а именно: п cost п cos- i Q. g2* (1.55*) Случай нескольких центрированных поверхностей. Фокусы сагиттального и меридионального пучков, полученные после „ 33 о г. г. Слюсарев преломления через одну поверхность, являются вершинами пучков, падающих на следующую поверхность. Поэтому задача нахождения положения астигматических фокусов после преломления через оптическую систему решается повторным применением формул (1.52) для меридионального и (1.55) для сагиттального пучков. Обозначим по-прежнему через к номер преломляющей поверхности. Формулы (1.52) и (1.55) с добавлением значка к у величин п, i, tin, ts, г, п , i , tin и ts дают положение фокуса преломленного пучка по известному положению фокуса падающего пучка. К ним нужно еще присоединить формулу перехода от поверхнос1;и с номером к к поверхности с номером к+1. Пусть (рис. 1.13) точка М = представляет фокус сагиттального (или меридионального) пучка, преломленного через поверхность с номером к; тогда, очевидно. 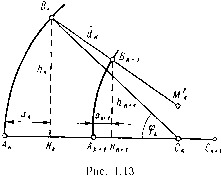 где dif, - так называемая косая толщина между поверхностями к и к + 1 (расстояние по главному лучу между точками пересечения луча с поверхностями к и к: + !)• Обозначим высоты пересечения поверхностей к и к + 1 с главным лучом НВ Hk+i§k+i через и A+i и соответствующие им стрелки ЛЯ и Л+хЯх+х - через и uk+i- Величина d может быть получена по формуле 4 = {fiK - K+i) cosec Uki, (1.56) = r«sincp« = rsin {uk - Q = r«sin(u« -tJ. Для малых углов u+i лучше пользоваться формулой 4 = Йк + йк -Ak+i, fl« = 2r«sin. Формулы Аббе не очень удобны для вычислений при помощи логарифмических таблиц, так как формулы (1.52) и (I 55) мало пригодны для приведения их к логарифмическому виду и при помощи арифмометра, так как число умножений и делений велико Однако при вычислениях с помощью ЭВМ формулы Аббе доста- ажа-визны удобны; их преимущество заключается в том, что они при-ны и для несферических поверхностей. В последнем случае для меридиональных пучков следует вместо писать г (радиус tpHBH3Hbi меридионального сечения преломляющей или отр ющей поверхности), а для сагиттальных - rs (радиус крив сагиттального сечения этой же поверхности). Для плоскопараллельной пластинки с толщиной d и показателем преломления п формулы Аббе приводят к особенно простым вычислениям. Пусть (рис. 1.14) на пластинку падает луч, Ьбразующий с осью угол Ul и абсцисса точки-фокуса Ml (сагиттального или меридионального) относительно первой поверхности призмы равна Xi. Найдем х1 - абсциссу соответствующего фокуса Мг, после преломления через пластинку. Замечая, что Ui = i. = i„. и. == «1, = Рис. 1.14 = d sec «2. 1 = 1 s "i L = 4 sec u, и применяя последовательно формулы (1.52), (1.55) и (1.55*), получаем .x;.2s = Xis---- i cosu. я COSM2 d cos «1 rt cos «2 (1.57) Преломление через плоскопараллельную пластинку вызывает смещение фокусов в направлении оси на величину А = " + + d. Подставляя вместо х только что найденные значения, находим для смещения сагиттального фокуса cos tfi cos U.J для смещения A,„ меридионального фокуса 1 cos A,„ = d(l- n cos «2 / (1.58) • Пластинка вызывает, кроме того, смещение Ay фокусов в на-правлении, перпендикулярном к оси. Обозначим через и ординаты фокусов Мх и М2 до и после преломления. Замечая, что = ОЛ; - tg «j, a Уз = О2Л2 - x tg и, получаем у; - у = Ау=. 0 - ОД - (х; - Xj) tg u, = = -dtgu -(х; -Xj) tg«i. Для смещения сагиттального фокуса находим Ду =у; у - dtgu., + -5tgu, = »s »2 -1 2 I n COSUa 1 d sin u. , , =--- - d\"Uo = 0, n CCS «2 " так как sin u-i --= n sin u„; для смещения меридионального фокуса получаем А J i , d cos u, , ДУ„ = Уз - У1 = tg «2 + ~ tg u, = - \ CDS (b Окончательно Ауз = 0; Ay,„ = d tg /Л, - cos- M, -1 - sin M, = cf («2 1) tg H„ = d (n2 1) ----------. (1.59) Как осевые, так и поперечные смещения фокусов нлоскопарал-лельной пластинкой не зависят от Xi, т. е. от положения пластинки, а зависят только от ее толщины, показателя преломления и наклона главного луча к передней грани. 5. РАЗНОСТНЫЕ ФОРМУЛЫ Разностные формулы для сферической аберрации Кербер вывел две формулы, позволяющие получить сферическую аберрацию и отклонение от закона синусов оптической системы, не прибегая к обычному способу, который заключается в вычислении хода луча с больши.м числом знаков по основным формулам (1.1)-(1.5) с последующим вычитанием координат параксиального луча, рассчитанного с такой же точностью, как первый луч. Вместо этого результат получается сложением сравнительно малых величин, по существу являющихся аберрациями луча для каждой поверхности системы, новные формулы (1.1)~(1.4) приводят к следующему выра-ию: Г--S = (г - s)~-r-г, (1.60) ft sin и \ причем [см. формулу (1.3)] и = и i - i. • Введем величину D, определив ее из уравнения sin«= sin и + sin Г - sint + D. (1-61) Разложив в этом уравнении синусы всех углов в ряды и приняв во внимание (1.3), убеждаемся, что D - величина третьего порядка малости относительно углов и, и, i и г. Замечая, что sin Г - sin t = (- - 1) sin ( получаем из (1.61) sinu == sin ы + ("5"- - sin и. - sin U + D. Из формулы (1.60) находим и заменяем sin а только что полученным выражением; это дает г - S п г - S г - S п sin u (1.62) Перепишем эту формулу для параксиальных лучей, обозначая через S, и s, расстояния от вершины поверхности до точек пересечения луча с осью до и после преломления, получаем 1 « 1 п -п 163) п г - So так как отношение при беспредельном уменьшении и В силу сделанного замечания относительно величины D стремится к нулю. Вычитая (1.63) из (1.62), получаем s n sin u 6s= s- So и 6s = s -So-Обозначим углы, образуемые параксиальным лучом с осью системы до и после преломления, буквами а и а ; на основании (0) (1) (2) (3) (4) ( 5 ) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|