
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) ( 55 ) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (55) Кельнера может отстоять от последней поверхности на /2 фокусного расстояния, т. е. дальше, чем у окуляра Рамсдена, но ближе, чем у симметричного и ортоскопического окуляров. Поле зрения окуляра Кельнера достигает 50°. 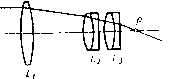 Рис. V.18 Рис. V.19 Окуляры широкоугольные составлены из трех линз, из которых одна простая, а две - двойные,.благодаря чему высшие поряцки аберраций наклонных пучков уменьшены. Существует 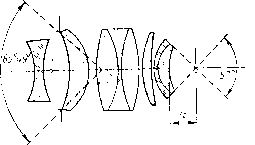 Рис. V.20 несколько вариантов широкоугольных окуляров, из которых наиболее удачными нужно считать типы, предложенные Эрфле. Первый тип Эрфле (рис. V.18) является усложнением окуляра Кельнера путем раздвоения глазной линзы LgLg-, оба компо- 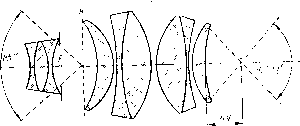 Рис. V.21 нента L, и Lg одинаковы. Поле зрения достигает 60-65 ; при увеличении поля дисторсия и хроматическая разность увеличении превышают допустимые значения (8-10% для дисторсии). Расстояние зрачка от последней линзы 0,5-0,6 фокусного расстояния, как и в окуляре Кельнера. Второй тип Эрфле (рис. V.19) можно рассматривать как симметричный окуляр/с прибавлением третьей линзы в середине, цель которой - уменьшить аберрации высших порядков. Поле зрения не превышает 60°, но расстояние до зрачка достигает фокусного расстояния. Существуют еще и другие типы окуляров, впрочем, мало применяемые, например окуляры с далеко вынесенным выходным зрачком (бинокли, Прицелы и т. д.). Простейшим способом удаления выходного зрачка является введение отрицательного компонента на небольшом расстоянии от переднего фокуса окуляра. Нужно, однако, иметь в виду, что чем дальше отстоит выходной зрачок, тем меньше поле зрения (при одном и том же типе окуляра). На рис. V.20 и V.21 приведены схемы двух особо широко-угольных окуляров, обладающих углами поля 85°. У первого из них (/• = 15, 1 : 4,3, 2р = 86°) выходной зрачок находится на расстоянии, равном фокусному. У второго (/ =30, 1 : 5, 2р = 85°) расстояние до зрачка равно 1,6 фокусного расстояния, что достигнуто применением параболоидальной поверхности. Несмотря на необычно большие значения угла поля зрения и удаления зрачка выхода, качество исправления аберраций хорошее. Сообщенные краткие сведения дают возможность составить предварительный проект оптической системы. Однако могут представиться случаи, когда из-за каких-нибудь условий, чаще всего габаритного характера, представляется необходимым перейти через указанные здесь пределы; тогда расчет системы, удовлетворяющий необычным требованиям, делается очень трудным и сложным. ГЛАВА VI МЕТОДИКА РАСЧЕТА ОПТИЧЕСКИХ СИСТЕМ 1. ВВЕДЕНИЕ Рассчитать оптическую систему - это значит определить конструктивные элементы (радиусы кривизны или профили сечений преломляющих и отражающих поверхностей, толщины линз, расстояния между оптическими элементами, световые диаметры линз и зеркал, сорта применяемых стекол и т. д.), допустимые отклонения от величин этих элементов и отступления от идеальной центрировки. Могут быть еще и другие элементы расчета в зависимости от назначения и действия прибора, для которого рассчитывается оптика. Существует несколько основных методов расчета, на выбор которых влияют многие обстоятельства - от личных вкусов конструктора-вычислителя до характеристик оптических систем (например, их относительные отверстия и величина угла поля зрения). Немалую роль играет и наличие или отсутствие тех или иных вспомогательных средств вычисления: арифмометров, быстродействующих электронных машин и т. д. После довольно длительного периода использования эмпирических методов изготовления первых нашедших применение оптических приборов: луп, очковых стекол, зрительных труб и микроскопов - начались попытки перехода к более обоснованным методам, опирающимся на знание законов преломления и отражения. Неудивительно, что Декарт, сформулировавший впервые точные законы преломления и отражения, стал первым оптиком-конструктором, указавшим на наличие сферической аберрации линз и показавшим, как ее исправлять. Ньютон, открывший дисперсию и хроматическую аберрацию линз, дал и формулы для оценки последней, которые значительно позже позволили Дол-лонду создать первые ахроматы. Эйлер написал большой трактат о расчете оптических систем («Диоптрика»), в котором была приведена целеустремленная методика расчета, не нашедшая впоследствии применения только потому, что она опиралась на неверную гипотезу о значении дисперсии материалов и не принимала во внимание одну из главнейших аберраций оптических систем - кому, о существовании которой во времена Эйлера никто не знал. 334 Следующий шаг в направлении разработки методики расчета был сделан австрийским математиком Пецвалем. После того как он получил путем весьма трудоемкого разложения в ряд выражения для аберраций третьего и пятого порядка (а может быть и дальше - все его работы пропали при пожаре), он убедился в невозможности использования плодов своих трудов из-за их слишком большой сложности и создал метод проб, основанный на изучении связи между аберрациями системы, вычисленными с помощью расчета хода лучей, и некоторыми ее конструктивными элементами. С помощью этого метода Пецваль рассчитал первый светосильный фотографический объектив (1840 г.), названный его именем. Впрочем, этот объектив любопытен тем, что в нем так называемое условие Пецваля, т. е. условие отсутствия кривизны изображения, не только не выполнено, но, наоборот, кривизна больнке, чем у всех ранее известных объективов. Несколько позже (1856 г.) Зейделем были выведены и опубликованы формулы для коэффициентов аберраций третьего порядка, но Зейдель, как и Пецваль, пришел к выводу о невозможности использования этих формул для практических вычислений из-за их крайней сложности. Лишь в начале XX в. непрекращающиеся попытки найти применение формулам Зейделя привели к успеху в простейшем случае двухлинзового объектива, который представлял весьма значительный практический интерес, так как являлся основным компонентом подзорных труб любого рода, а также микроскопов слабого увеличения. Двухлинзовые объективы, наиболее часто встречающиеся на практике, обладают малым относительным отверстием, обычно меньше чем 1 : 4- 1 : 5; вследствие этого толщины линз малы по сравнению с фокусным расстоянием и аберрации высших порядков намного меньше, чем аберрации третьего порядка; наконец, угол поля зрения мал, а следовательно, для получения хорошего качества изображения достаточно исправить две аберрации - сферическую и хроматическую. Благодаря этому оказалось возможным получить довольно простые формулы для радиусов кривизны поверхностей при известных характеристиках применяемых оптических стекол. Задача расчета двухлинзовых объективов решалась неоднократно многими исследователями, пользовавшимися различными переменными и принимавшими во внимание большее или меньшее количество дополнительных условий. Более того, рещение этой задачи стало своеобразным критерием, позволяющим оценить возможности того или другого предложенного метода. Прошло более 60 лет после опубликования первых работ, посвященных этой задаче, но и в настоящее время поступают в печать новые и новые работы на эту же тему. . Подобные исследования положили начало второму методу расчета оптических систем, который получил у нас название алгебраического метода - в противовес описанному ранее тригонометрическому, основанному на изучении результатов вычисления с помощью таблиц тригонометрических величин с последующим интерполированием (или экстраполированием). В этой главе будет рассматриваться лишь алгебраический метод, а метод проб, получивший большое развитие после появления и освоения ЭВМ, будет изложен в гл. VII. 2. ОСНОВНЫЕ УРАВНЕНИЯ АЛГЕБРАИЧЕСКОГО МЕТОДА Как было изложено выше, алгебраический метод возник после того, как на примере двухлинзового объектива выяснилась полная возможность расчета оптической системы, исходя из формул для коэффициентов аберраций третьего порядка. Нетрудно было распространить этот метод на расчет простых линз, двухлинзовых несклеенных и трехлинзовых склеенных объективов и вообще бесконечно тонких компонентов, хотя при увеличении числа линз растет число неизвестных и простота решения исчезает. Более того, методика алгебраического расчета могла быть без труда распространена на тот случай, когда оптическая система состоит из нескольких компонентов (например, объектива и окуляра или объектива, оборачивающей системы линз и окуляра) или представляет собой зеркальную или зеркально-линзовую систему из нескольких зеркал и линз. Как было показано в гл. III, все поперечные аберрации третьего порядка монохроматических лучей, а также обе хроматические аберрации параксиальных лучей (хроматические аберрации положения и увеличения) центрированной оптической системы могут быть представлены как сумма произведений вида 8g = S m,P; + S tiiWi + S рщ + S g,; 8G = m\Pi + + S Pii + S-?;- для аберраций монохроматических лучей и sf - sc = riCi\ (VI.1) (VI.2) для хроматических аберраций. При этом величины /л,-, п,-, п., . . ., г., г, зависят только от оптических сил компонентов, расстояний между ними, апертуры системы и расстояния точки-объекта от оси, а величины Pi, Wi, л, q„ Cj связаны с конструкцией элемента i, т. е. с его радиусами кривизны, показателями преломления и коэффициентами дисперсии (для С,-), а также с положением объекта относительно компонента i. Однако в гл. 1П было показано, что параметры Р, и Wi, зависящие от положения предмета, можно заменить теми же параметрами, связанными только с конструктивными элементами; при этом зависимость и от Р( и Wj линейная, и вид уравнений (VI. 1) и (VI.2) остается без изменения, но переход от старых Pi я Wi к новым Р,- и позволяет осуществить полностью разделение параметров на две группы. В первую группу входят внешние величины, связанные с габаритными характеристиками системы, силы отдельных компонентов, расстояния между последними, диаметры их, зависящие от апертурных и полевых углов, как это было показано в гл. V. Поэтому эти величины можно считать известными. Параметры второй группы Р, W, я я С получаются из решения системы уравнений (VI. 1) и (VI.2), если правые части этих уравнений известны. Определение этих правых частей, а также числа уравнений систем (VI.I) и (VI.2) будет рассмотрено ниже. Составление уравнений, их решение Напомним формулы (11.42*) для всех аберраций третьего порядка оптических систем с осевой симметрией: 1) для сферической аберрации - 2np8gi = СОр (СОр Qp)Si, - 2пр80[ = Qp {(Op + Qp) S,; 2) для комы - 2np8gn = {Зсор -f □;) wSif, ~2np8Gii = 2u)pQpWiSii\ 3) для кривизны поляки астигматизма - 2np8gni+i = (o>?(3Sm +/S,v); - 2«p6Gni+iv = «pt£)?(Siii +/Siv); 4) для дисторсии - 2np8gv = w\Sv; - 2np8Gy = 0. (VI.3) В этих формулах 8g я 6G - проекции на меридиональную и экваториальную плоскости отрезка 8L, соединяющего точку пересечения луча с гауссовой плоскостью изображения с точкой, изображающей по законам гауссовой оптики рассматриваемую точку-объект, в том предположении, что все аберрации, за исключением Т-я, уничтожены. В особо важном случае, когда плоскость предмета находится на бесконечности, удобнее всего пользоваться формулами (III.7*), 22 г. г. Слюсарев 337 (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) ( 55 ) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
||||||||||||||
|
|