
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) ( 65 ) (66) (67) (68) (65) Решим систему (VII.26) и найдем значения изменений коррекционных параметров Ар*/. Внесем эти изменения в исходную систему, произведем расчет значений функций, соответствующих значениям коррекционных параметров, равным pf> + Ар, р(") + Ар(1), . . ., р°> + Если значения всех функций ока- жутся внутри заданных интервалов Фх ± бФ, Фа ± АФа, . . ., Фк ± бФк, то решение задачи окончено. В противном случае система, полученная после первого приближения, принимается за исходную для следующего приближения и процесс повторяется вновь. Определение частных производных необходимых для составления системы линейных уравнений (VI 1.26), может быть произведено двумя принципиально различными способами. Один способ основывается на применении точных формул для производных -д, получаемых путем установления дифференциальных соотношений между конструктивными элементами оптической системы и параметрами, определяющими положение лучей. Другой способ нахождения производных основывается на использовании метода конечных разностей. Каждый из коррекционных параметров системы поочередно изменяется на некоторую малую величину бр(, а затем по точным формулам производится вычисление новых значений функций, соответствующих измененной системе. С некоторой степенью точности можно принять, что частные производные равны частным от деления приращений функций на приращения соответствующих параметров: (VII.27) где ф. значение функции, соответствующее значениям] коррекционных параметров, равным р<°), . . ., pf* + бр., pf, п(0) > Рк Так как при разложении функций Фу в ряды были опущены члены, содержащие производные выше первого порядка, область применимости системы линейных уравнений (VII.26) ограничивается малыми изменениями параметров. Однако при решении системы линейных уравнений (VI 1.26) изменения параметров Арр, вообще говоря, могут получиться сколь угодно большими и их введение в исходную систему приведет к абсурдным результатам. Рассмотрим определитель системы уравнений (VII.26):
= D. (VII.28) следующих условиях определитель может обратиться При в нуль: I. В определителе D имеется хотя бы один столбец, элементы которого представляют собой линейную комбинацию соответствующих элементов каких-либо других столбцов. В частном случае элементы одного столбца пропорциональны элементам другого столбца. Параметры, соответствующие этим столбцам, могут быть названы эквивалентными, поскольку частные производные от функций Ф/ по этим параметрам связаны между собой зависимостью дФ, dpi дФ, дрт дФ, йФ, дФк дФк dpi др„ dpi dpn (VI 1.29) где Pi и p,„ - эквивалентные параметры. 2. В определителе D имеется хотя бы одна строка, элементы которой представляют собой комбинацию соответствующих элементов каких-либо других строк. В частном случае элементы одной строки пропорциональны элементам другой строки; тогда функции, соответствующие указанным строкам, являются взаимно зависимыми. 3. В определителе D имеется хотя бы один столбец, элементы которого равны нулю. В этом случае параметр, соответствующий этому столбцу, не влияет на изменение функций. 4. В определителе D имеется хотя бы одна строка, элементы которой равны нулю. В этом случае функция, соответствующая этой строке, не зависит ни от одного нз коррекционных параметров. На практике, поскольку мы имеем дело с численным методом, яи один из перечисленных случаев в чистом виде не встречается. Однако приближенное выполнение всех, а в особенности первых 1вух условий, встречается нередко. Это приводит к малым значениям определителя D и большим изменениям параметров Ар.>. Поэтому метод Ньютона применим только в тех случаях, когда Исходная система близка к заданной. Кроме того, при использо-!вании метода Ньютона необходимо осуществлять контроль за Сходимостью итерационного процесса. Условия сходимости исследованы математиками детально, но эти условия весьма сложны, и для проверки их выполнения необходимо произвести большие вычисления. Поэтому в программах, основанных на ме годе Ньютона, проверка сходимости осуществляется после каждой терации. Рассмотрим некоторые способы проверки сходимости. Представим себе пространство функций Ф/. В этом пространстве исходной оптической системе соответствует некоторая точка, координатами которой являются значения функций Ф[\ Ф>, . . ., с1)(,0). Искомой оптической системе соответствует точка с координатами Ф1, Фа, . . , Фк. являющаяся центром многомерного параллелепипеда, грани которого равны удвоенным значениям допусков на значения функций. Так как функции могут в принципе иметь различную размерность, то рационально принять такую метрику пространства, в которой единицами измерения по отдельным координатным осям служат допуски на функции, т. е. величины бФ/. Тогда искомой оптической системе в пространстве функций будет соответствовать многомерный куб, каждая грань которого равна двум единицам. Для пояснения сказанного служит рис. УП. 2, где представлено пространство, образованное двумя функциями Ф и Фа-Расстояние между заданной и исходной точками может быть вычислено по формуле 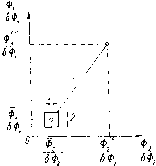 Рис. VI 1.2 /=-1 (VII-.30) Изменение этого расстояния после очередного шага постепенных приближений может быть принято в качестве критерия сходимости. Действительно, если с каждой итерацией это расстояние сокращается, то можно утверждать, что процесс не расходится. Если расстояние L начинает расти, то процесс следует прекратить, так как это может означать появление расходимости. Таким образом, после очередного шага постепенных приближений произ- водится вычисление величины ~ ~ 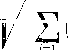 S-порядковый номер шага, и сравнение ее с величиной Ь 1. Если Ls<Ls i, то процесс расчета можно продолжать. Если Lj 5= Ls i, то расчет следует прекратить. Другой способ контроля сходимости основывается на рассмотрении пространства коррекционных параметров. В этом пространстве, в отличие от пространства функций, координаты точки, соответствующей искомой системе, заранее никогда неизвестны. Поэтому контроль сходимости в этом пространстве может быть осуществлен по изменению расстояния между точками, соответствующими двум последовательным итерациям. Это расстояние может быть вычислено по формуле (VII.31) где Ар(* - результаты решения системы линейных уравнений (УП.26). Если Ps<Ps-i (где и P.i - значения для итерационных шагов с порядковыми номерами s и s - 1), то процесс расчета следует продолжать. В противном случае процесс может расходиться и его следует прекратить. Изложенный метод был реализован в одной из программ, предназначенных для автоматического расчета оптических систем в области аберраций третьего порядка. Программа была составлена В. А. Ефимовым под руководством Н. Н. Губеля. В таких программах в качестве функций Ф/ рассматриваются коэффициенты аберраций третьего порядка Si, Su, Sm, Siv, Sv, St", Su и такие параксиальные характеристики системы, как s - расстояние изображения от последней поверхности - я х - расстояние выходного зрачка от последней поверхности. Программы такого рода находят в настоящее время широкое применение, что объясняется двумя причинами. Во-первых, расчет коэффициентов аберраций третьего порядка занимает примерно в три раза меньше времени, чем расчет минимально необходимого количества лучей, с помощью которых могут быть установлены примерные значения аберраций третьего порядка. Это, с одной стороны, позволяет использовать для расчета машины, обладающие невысокими скоростями работы, а с другой стороны, дает возможность в сравнительно короткие сроки и с малыми затратами машинного времени произвести исследования большого количества различных вариантов системы в области аберраций третьего порядка. Во-вторых, зависимости между коэффициентами аберраций третьего порядка и параметрами системы ближе к линейным, чем зависимости между точными значениями аберраций и параметрами. Поэтому при автоматической подгонке заданных коэффициентов аберраций третьего порядка сходимость итерационного процесса, как правило, оказывается лучшей, чем при использовании в качестве функций точных значений аберраций. Приведем два примера расчета по рассмотренной методике. Расчеты выполнялись на электронной вычислительной машине «Урал-2», обладающей скоростью, равной примерно 5000 операций в секунду. Первый пример представляет собой расчет апохроматического объектива с небольшой числовой апертурой. Объектив состоит из двух двусклеенных компонентов, разделенных значительным воздушным промежутком, т. е. выполнен по схеме Пецваля. Схема объектива представлена на рис. УП.З. Задача состоит в том, чтобы Рис. VII.3 путем замены материалов, из которых выполнены линзы в ранее рассчитанном ахроматическом объективе, получить объектив с апохро-матической коррекцией. Исправлению подлежат сферическая аберрация кома (Su), астигматизм (Sm) и хроматизм положения (Sfp). В качестве коррекционных параметров используются углы первого параксиального луча с осью а,-, а не радиусы оптических поверхностей. Такой выбор параметров не случаен, так как позволяет поддерживать постоянным в процессе расчета фокусное расстояние системы или ее увеличение. Конструктивные параметры исходного ахроматического объектива приведены в табл. УП.2. Таблица VII.2 Для получения апохромати-ческой коррекции заменим стекла К8 и КФ4на флюорит. Стекла БФ12 и ТФ1 заменим таким образом, чтобы в каждом компоненте примерно сохранилась разность показателей преломления, а коэффициенты дисперсий V удовлетворяли бы следующему соотношению: -= const, (Vn.32) где - крэффициент дисперсии стекла положительной линзы; Уф - то же стекла отрицательной линзы. Такое правило подбора стекол позволяет получить в каждом компоненте при параметре С = О примерно такое же значение параметра Р,, какое было в исходной системе, и обеспечивает большую вероятность успеха, чем произвольный выбор, поскольку поставленная задача имеет решение отнюдь не при любых комби нациях стекол. В результате стекло БФ12 может быть заменено стеклом БФ4 а стекло ТФ1 - стеклом БКЮ. Обратим внимание также и на то что стекла БФ4 и БКЮ имеют частные относительные дисперсии близкие к частной относительной дисперсии флюорита. Это поз
волит получить систему с небольшим вторичным спектром Зададим S, = О ± 0,1; 5„ О ± 0,1; 5,„ = О ± 0,1; S-p = О ± 0,005. Коэффициенты аберраций будем вычислять при нормировке а = = 1; /ij = / = 20. В качестве коррекционных параметров используем «2. «3, «5 и а. Результаты расчета на машине «Урал-2» приведены в табл. УП.З. Таблица VII.3
В последней строке таблицы УП.З даны значения величины (УП.ЗО), с помощью которой в программе контролируется сходимость итерационного процесса. На решение задачи затрачено около одной минуты машинного времени. В качестве второго примера рассмотрим расчет фотографического объектива типа триплет. Этот пример позволяет весьма наглядно сравнивать между собой различные методы расчета и поэтому неоднократно использовался в качестве теста при проверке программ. Конструктивные параметры исходной системы выбраны произвольно. Марки стекол и задаваемые значения коэффициентов аберраций взяты из системы, расчет которой был произведен в 30-х годах. Как видно из табл. У 11.4, итерационный процесс начинает сразу же расходиться, несмотря на то, что решение существует. Для наглядности в таблице приведены два итерационных шага. Пример показывает, что метод Ньютона неприменим в тех случаях, когда значения параметров в исходной системе существенно отличаются от таковых в системе с заданными коэффициентами (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) ( 65 ) (66) (67) (68) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|