
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) ( 66 ) (67) (68) (66) Таблица VII.4 Заданные значения коэффициентов аберраций Sj-=1,9±0,1 Sj, = 0,3 ± 0,05; S„i -0,2 ± 0,02; Sjv = 0,43 ± 0,01; S. О ± 0,01; Р -~= О ± 0,001; Sff = 0± 0,001 Расстояния между вершинами поверхностей в исходной систе.че di-0,05; da = 0,1; dg - 0,02; d4 = 0,l; d5 = 0,05 Марки стекол Параметры и функции «3 «4 «в ТК16; БФ12; TK16 Исходные значения 1-я итерация 2-я итерация Система с заданными коэффициентами
tti = 0; hy --= = -0,03; a, == аберраций. Для сопоставления в последнем столбце табл. VII.4 даны значения коррекционных параметров в системе, обладающей заданными коэффициентами аберраций. Расчет производился на машине «Урал-2». Первая модификация метода Ньютона Для улучшения, сходимости итерационного процесса при использовании метода Ньютона были разработаны и нашли практическое применение несколько модификаций. Рассматриваемая здесь модификация [6-8] была положена в основу одной из программ для автоматического расчета оптических систем в области аберраций третьего порядка. Эта программа, составленная применительно к машине «Урал-2», с успехом эксплуатировалась в течение нескольких лет рядом организаций. Попытки использовать ту же методику для автоматического расчета оптических систем в области точных значений аберраций оказались неудачными из-за медленной сходимости итерационного процесса во многих случаях. Основная цель модификаций метода Ньютона заключается в предотвращении расходимости итерационного процесса. Сущность этих методов состоит в том, что каждый шаг итерационного процесса разбивается на два этапа, первый из которых представляет собой выбор направления движения (определение соотношения между изменениями параметров), а второй этап - выбор величины шага в этом направлении. Направление движения опреде-дяется путем решения системы линейных уравнений (VII.26). Выбор величины шага осуществляется путем анализа изменений функций при движении в найденном направлении. Введем понятие величины шага i[i. Изменения параметров, соответствующие величине шага г(), вычисляются путем умножения изменений параметров Др*., полученных в результате решения системы линейных уравнений (VII.26), на if, т. е. Др1 = г)ДрР, Ар2 = г)Ар\ . . ., Арг = г5АрГ\ . . ., Арк = г;Api, После выбора направления движения функции Ф/ зависят лишь от величины шага, т. е. от переменной Во избежание расходимости итерационного процесса условимся выбирать таким образом, чтобы после выполнения очередной итерации с порядковым номером S разности Ф) - Ф,- убывали по абсолютной величине. В то же время для уменьшения количества итераций необходимо, чтобы каждая из функций Ф, при каждой итерации максимально приближалась к заданному значению. Наиболее простой способ определения величины шага по этим правилам заключается в следующем. Выбрав некоторое достаточно малое значение i()i для величины ф, можно последовательно шаг за шагом вносить в исходную систему изменения параметров, соответствующие сначала затем 2i:(), затем 3i)i) и т. д., и вычислять при этом по точным формулам значения функций Ф;. В тот момент, когда одна из функций достигнет заданного интервала значений от Ф,- - 8Ф/ до Ф,- + бФ/ или когда какая-нибудь из функций примет экстремальное значение, процесс подбора следует прекратить. Полученная при этом система может использоваться как исходная для следующего приближения. В целях ускорения определения величины шага используется следующий способ. Разложим приращения функций Ф. - Ф0) в ряды по степеням г): и ограничимся первыми двумя членами разложения. Тогда получим dOi , , 1 фГ Ф,.-Ф) (0) дФк 2 дМ (Vn.33) Очевидно, значения производных, входящих в выражения (Vn.33), могут быть определены методом конечных разностей, если известны значения функций Ф/, соответствующие каким-либо двум значениям ф. Заметим, что поскольку формулы (УП.ЗЗ) являются приближенными, то при нахождении производных Щ- следует пользоваться значениями , соответствующими малым значениям приращений параметров. Один из возможных способов выбора этих значений состоит в следующем. Пусть бр1, бра. • • . брь . . ., Ьр - некоторые достаточно малые приращения параметров, например те, которые используются для определения частных производных от функций по параметрам р,-. Вычислим абсолютные значения отношений (VII.34) и выберем из них наименьшую величину, которую обозначим через г5(>. Очевидно, что если положить ф = то изменения параметров Api при этом не превысят соответствующих величин бр(. Вычислим по точным формулам (в частности, с помощью расчета хода лучей) значения функций Фр соответствующие г) = , т. е. для значений параметров р(°) + i:(i)Apji); р») + фАр), • •> Рк* -fФ*Ар1), и обозначим их через Ф\\ Ф(1), ... ,ф(1.1) Вычислим также значения функций Фу, соответствующие i: = гф*! и обозначим их через ф(.2), ФП.г), . . фа.2). Тогда, воспользовавшись (Vn.33), находим, что ЙФу (Эф 4ф(.1.1)-ф(.1.2) -ЗФ(0) (VII.35) дЩ ф)->-2ф.1) + ф(.0) ШЧ (VII.36) После замены JB (УП.ЗЗ) текущих значений функций Фу на заданные значения Фу каждый из к рядов можно рассматривать как квадратное уравнение и решать относительно . Обозначим г):, найденное из /-Г0 уравнения, через \;у. Тогда <ЭФу (VII.37) Для определения знака перед корнем в выражении (УП.37) установим зависимость между величинами и Фу - ФК Рассмотрим одно из уравнений системы (УП.26) 1=1 (VII.38) Умножим обе части равенства (УП.ЗВ) на d\. Тогда <=/с (ф. ф(.о)) = с/г; 211 АрГ и (Фу - Ф°0 rfol, = dФi, зткуда следует, что = Фу-Ф} ,(0) (VII.39) Поскольку вычисление -ф- и производных ЛГ " ьии.зоидпыл -д- осуществляется с помощью приближенного метода конечных разностей. дФ,- .(0) го значения совпадут со значениями приращений Ф,- - ф} лишь приближенно. Несмотря на это, выражение (VII.39) может служить хорошим средством контроля правильности вычислений, а также правильности выбора величин бр,-. 26 г. г. Слюсарев 401 Итак, на основании (УП.39) выражение (УП.37) можно преобразовать к виду (V11.40) - 1 + откуда видно, что знаку плюс перед квадратным корнем всегда соответствует меньший по абсолютному значению корень квадратного уравнения. Так как ряды (VII.33) справедливы лишь при небольших значениях , то корень, соответствующий знаку минус в выражении (VI 1.40), как имеющий большее абсолютное значение, вообще не следует принимать во внимание. Покажем, что выбранный корень всегда положительный. Если • > о. то подкоренное выражение в (VI 1.40) больше единицы, а выражение в круглых скобках больше нуля. Следова- < О, то подкорен- тельно, также больше нуля. Если . --2 ное выражение меньше единицы, а выражение в круглых скобках меньше нуля. Следовательно, % снова больше нуля. В случае отсутствия вещественных корней для какого-либо /-Г0 уравнения, т. е. в том случае, когда 1 + 2 . -щ-следует найти величину i>j ext, , при которой значение функции Ф, максимально приближается к заданному значению Ф,-. Из (VII.33) нетрудно получить, что дФ,- . <ЭФ <0, ф; ext.- = - (VI1.41) Очевидно, что и %extr > 0. Решив все к квадратных уравнений, получим к значений Выберем из них наименьшую величину, которую обозначим через Нетрудно показать, что при = г)„ для всех функций будет выполняться следующее соотношение: ф(1) ф(.о) О «Г" - - ф. ф(0) (VII.42) .д ф!) значение функции Фу при = \рпм- Для доказательства преобразуем выражение (VII.40), приняв во внимание (VI 1.41): (VII.43) >0 = %extr / extr Поскольку, как было показано, г)у > О, то при 1 < /extr- Если 1 + / extr < О, ТО г:у = г:уех1 Ф extr Отсюда сле- дует, ЧТО i:yextr, а это означает, что в интервале от i: = О до = % функция Фу изменяется монотонно. Поэтому, поскольку %м < ТО все функции в интервале от г; = О до г; = изменяются монотонно. Следовательно, на основании (VII.43) можно утверждать, что значен21е Ф) любой функции будет заключено в интервале от Ф{° до Фу. Этим самым доказана справедливость выражения (VII.42). Итак, при \1р = значения всех функций с точностью, с которой справедливы ряды (VI 1.33), будут лежать внутри интервалов отФ)" до Фу, т. е. при г; = -ф, все функции приближаются к заданным значениям. Внесем в исходную систему изменения коррекционных параметров, соответствующие г5„«, т. е. Api = Ар{\ Ар = = нм Р2 \ •, Ар,, = г)„„Ар>. Рассчитаем по точным формулам значения функций в системе с измененными значениями коррекционных параметров и проверим, не находятся ли значения всех функций внутри заданных интервалов Ф1 ± 6Ф1, Фг ± бФ.2, . . . , Фк± бФк. Если это условие выполнено, то расчет прекращается. В противном случае система с измененными значениями коррекционных параметров принимается за исходную для следующего шага постепенных приближений. Новый шаг 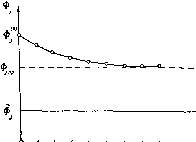 о 1 2 3 t 5 6 Рис. Vn.4 7 8 начинается с вычисления частных производных Затем шается система линейных уравнений и повторяются все операции, выполнявшиеся на первом шаге итерационного процесса. Расчет заканчивается тогда, когда все функции окажутся внутри заданных интервалов значений. Изложенный метод автоматического расчета в некоторых случаях не дает положительного результата. Это может означать, что поставленная задача вообще не имеет решения или что решение существует, однако из-за неудачного выбора исходной системы этот метод оказывается неэффективным. Как в первом, так и во втором случае наступает момент, когда приращения функций Фу, получаемые за один итерационный шаг, начинают резко уменьшаться по абсолютным величинам. Вычислительный процесс при этом сходится не к заданным величинам Фу, а к некоторым предельным значениям функций Фу„р, как это показано на pHc.Vn.4. Важно правильно установить момент, когда нужно прекратить вычисления, с тем чтобы не загружать машину бесполезной работой. Рассмотрим признак, который позволяет анализировать целесообразность продолжения итерационного процесса. 26* 403 (0) (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) ( 66 ) (67) (68) |
|
|