
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) ( 8 ) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (8) Действительно, пусть заданы параметры ц, v, fx и v. Параметры р. и V определяют совокупность параллельных лучей, падающих на систему. Среди этой совокупности лучей найдется один и только один, у которого после преломления через оптическую систему направляющие косинусы будут соответственно равны ц и v. Исключением является случай телескопических систем, когда может не оказаться ни одного луча с заданными параметрами или их может быть бесконечно большое число, если система идеально исправлена для данного направления. Зависимость углового эйконала от переменных р, v, р,, v. может быть установлена с помощью дифференциальных соотно-
шений, для вывода которых нужно рассмотреть новый луч R, бесконечно близкий к лучу R. Предположим, что в пространстве предметов луч К, параллелен лучу а следовательно, имеет те же р и V, что и луч R, но проходит через точку у dy, z + dz плоскости YZ. После преломления через оптическую систему луч Rl займет положение, определяемое косинусами р, + dp., v -f d\. В общем случае луч Ri в пространстве изображений не будет параллелен лучу R, но и не будет пересекать его. Найдем на обоих лучах две ближайшие точки: точку N с координатами X, F и Z на луче R и точку Nl с координатами X + dX ; V + + dY я Z -i- dZ на луче Ri. Отрезок N Ni есть кратчайшее расстояние между лучами R я Rl в пространстве изображений; он перпендикулярен каждому из них. Обозначим косинусы углов, образуемых лучом R с осями Ох, Оу, Oz, буквами К, р и v; эти косинусы связаны соотношением г + ii + v = 1. Соответственные косинусы для луча Ri будут равны Х + dk, jl + dp и v + dv. Опустим из начала координат О перпендикуляры: ОР на направление луча R и О Pi на направление луча Ri. Расстояни-я Np я N[pi, равные проекциям радиусов-векторов ОМ я 0\n на лучи R и Rl, очевидно, определяются формулами yVP=rX + pr + vZ; (П.2) N[p[ = {X + dl) (X + dX) + ill + dyi) {Y + dY) + + (v + dv)(Z + dZ). (11.3) Введем функцию VF, выражающую собой длину оптического пути между точками Р я Р в зависимости от значений р, р, v и V ; измененное для луча R\ значение той же функции W дает длину оптического пути между точкой (пересечением перпендикуляра OPi, опущенного из начала координат О на луч Ri) и точкой Р\. Согласно представлениям волновой теории света, лучи геометрической оптики суть нормали к поверхности световой волны; поэтому два бесконечно близких параллельных луча R я R в пространстве предметов можно рассматривать как нормали к элементу плоской волны, находящемуся в плоскости OPPi, в таком случае световые колебания в точках Р я Р имеют одинаковые фазы. В пространстве изображений точки ;V и iVi, лежащие на общем перпендикуляре N N\ к лучам R я R\, также принадлежат одному элементу поверхности волны и, следовательно, имеют одинаковые фазы колебаний. Согласно теореме Малюса, система лучей, ортогональных поверхности волны в пространстве предметов, сохраняет свойство ортогональности по отношению к поверхности волны после всех преломлений и отражений при прохождении ее через оптическую систему; поэтому можно считать, что отрезки PPi я N Ni лежат на поверхности волны, проходящей через систему. В этом случае оптические длины между точками Р и yv, с одной стороны, и точками Р\ и Ль с другой, одинаковы; поэтому приращение функции W определяется произведением п на разность путей, определяемых уравнениями (II.2) и (П.З), NiPx - np = к dX + р dY + V dZ + Х dX + Y dp + Z dv. При этом произведения второго порядка малости, конечно, во внимание не принимаются. В этой разности сумма первых трех членов X dX + p dY +v dZ = 0, Так как прямая N N\ перпендикулярна лучу с направляющими косинусами X, ц, v. Таким образом, dW = п (X dX + Y dp + Zdv). (П.4) в силу соотношения (ИЛ) Следовательно, откуда = п (Z -Xi ~XZ U.51 Геометрическое толкование правых частей уравнения (И.5) не представляет затруднений: они равны соответственно координатам Y, Z точки L пересечения луча с плоскостью YZ, что легко проверить, если в уравнение луча х - X у -У гг к " \\ v подставить х = 0. Тогда у и г получаются равныкш правым частям уравнения (И.5). С полющью точно таких же рассуждений люжно прийти к выводу, что где г/ и г - координаты точки пересечения луча R с плоскостью У*2 в пространстве предметов. Переписываем уравнение (И.5), учитывая геометрическое толкование: = -пу; - = -nz. (11.7) Системы уравнений (11.6) и (11.7) показывают, что если бы функция W (р, V, ji, v) была известна в явном виде, то, дифференцируя ее по одной из переменных, от которых она зависит, и подставляя в выражение этой производной численные значения V, \у, и v для рассматриваемого луча, можно получить координаты точки пересечения луча с плоскостью YZ (или YZ). Рассматривая ряд лучей, исходящих из одной и той же точки плоскости предмета, и вычисляя все производные и , соответствующие этим лучам, можно получить ряд значений для точек пересечения лучей с плоскостью изображения. Естественно брать за плоскости YZ и YZ плоскости предмета и изображения, что в дальнейшем и будет сделано. Таким образом, функция W определяет точку пересечения луча с плоскостью изображения, что является основной задачей 52 лового равны г точек пересечения лучей расчета хода луча. Однако функция W, за исключением очень 1алого числа не представляющих практического интереса случаев, не может быть выражена в конечном виде как функция от \i, V, fx и v; ее приходится выражать в виде ряда, расположенного по степеням р,, v, v. К этим вычислениям мы вернемся ниже. Если с чисто технической стороны применение теории эйконала для расчета аберраций не представляет каких-либо серьезных преимуществ по сравнению с методами, основанными на непосредственном применении элементарных формул тригонометрического расчета хода лучей, то необходимо отметить, что только эта теория позволяет получать очень ценные при расчете сведения общего характера об аберрациях (например, данные о числе независимых коэффициентов аберраций разных порядков тех или иных оптических систем). Общий вид выражений для аберраций третьего порядка Как следует из формул (11.6) и (11.7) производные от yrj эйконала W по направляющим косинуса.м (х, v, v соответственно координатам у ~.---,.,-.,,r, с плоскостями предмета и изображения. Пусть LL (рис. П.З) - центрированная оптическая система; 00 - плоскость предмета; ОО - плоскость изображений; РР и РР - плоскости входного и выходного зрачков; А - точка предмета, лежащая в мери-;Диональной плоскости на -расстоянии у =- I от оси; ABCDEF - луч, определяемый координатами т и М точки его пересечения с плоскостью входного зрачка; этот луч пересекает плоскость изображений ОО с точке УР, координаты которой у и г. Если бы система была идеаль- Гой, то мы должны были бы иметь у = f>y, z pz = 0. .. Отступления у - Ру 6g и г - Рг - бС представляют обой проекции на оси координат поперечной аберрации AF, %. е. расстояния между идеальным изображением Ло точки А р точкой пересечения .туча с плоскостью изображения. 1 Эти проекции суть функции от координат падающего луча /, m \ Л1 и от конструктивных элементов оптической системы OLL, е. от радиусов кривизны ее поверхностей, толщин и показателен [реломления линз, воздушных промежутков между линзами и [Сложения плоскостей предмета и входного зрачка. 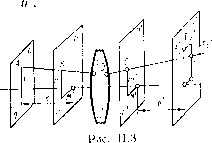 Считая систему известной, рассмотрим 6g и 6G как функции от одних только координат луча /, т, М, так что = hit, tn, М); бС = f{l, т, М). Вследствие симметрии системы относительно оси легко установить, что функции /i и /г не могут содержать членов четных порядков, как 1т, М, тМ и др.; присутствие таких членов нарушило бы выполнение условий /,(-/, -т, -M) = -f{l, т, /И); rn,-M) = ~l,(l, т, М) и т. д., обусловленных симметрией системы. Пусть е - расстояние от плоскости входного зрачка до плоскости предмета. Если /i {I, т. М) разложить в ряд Мак-лорена по величинам -у и которые мы примем за величины первого порядка малости, то получим** 4 fy,71 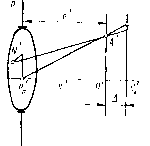 /1 (/, /п, М) = Oj - + Со - Рис. II.4 где = - частная производная от /1 по соответ- ствующая значению / = 0; а„ = (- - частная производная от /2 по -, соответствующая значению m О, и т. д.; ("Т") - частная производная от /j третьего порядка по / для значения / = О и т. д. Но коэффициенты Cj, а, Од равны нулю. Это вытекает из принципа Ферма, что легче всего показать следующим образом. В теории идеальных систем, а также реальных систем в параксиальной области было показано, что все лучи, исходящие из точки предмета, вновь сходятся в точку, лежащую в плоскости изображений. Рассмотрим, что происходит с изображением, если взять в качестве плоскости установки плоскость, отстоящую от плоскости О на величину Л. Такое изменение плоскости установки может улучшить качество изображения в тех случаях, когда имеются аберрации, и иногда называется дефокусировкой. Пусть Р (рис. П.4) - плоскость выходного зрачка системы; Pq - центр выходного 54 h (II.8) зрачка; А - изображение точки-предмета А параксиальными лучами; N - точка на выходном зрачке с координатами т и М. Найдем координаты у и г точки пересечения А" луча, проходящего через точку Ni, с плоскостью 0\, отстоящей от плоскости изображения О на величину Л и от выходного зрачка на е т- А. Уравнение луча NА имеет вид К -т Z - M у -И y = m + -:=X;Z Дадим X значение с 1- А. Тогда Y = тЧ- (У т)(\ +-)=у + {у->п)-; Z = M - M{1 + Изменение координат точки пересечения при переходе от старой плоскости О к новой еще не характеризует изменения картины, так как такому изменению подверглись координаты всех лучен, атом числе и главного луча PqA. Важны изменения, отнесенные к новому положению точки пересечения главного луча. Для главного луча координаты этой точки равны Y, = y+y Относительные изменения y-n = -m-; Z-Zo = -MA пропорциональны первым степеням координат т и М. Но для идеальных систем т = Рр/п; М = рМ, где Рр - линейное увеличение в зрачках. Для реальных систем приходится ввести поправки третьего порядка малости относительно величин -, -, которыми для принятой нами точности можно пренебречь, так как они умножаются на А - величину второго порядка малости, поскольку она такого ле порядка малости, что и продольные аберрации системы. Окончательно можно сказать, что изменение положения плоскости установки на величину А вводит аберрации bg=.-m%; бС = -МРрА (0) (1) (2) (3) (4) (5) (6) (7) ( 8 ) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
||||||||||||||
|
|