
 |
| Главная -> Книги (0) (1) (2) (3) (4) (5) (6) (7) (8) ( 9 ) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) (9) первого порядка малости. Отсюда можно сделать вывод, что наличие членов аберраций первого порядка малости свидетельствует о случайности выбора плоскости установки. Если за плоскость установки принять плоскость, сопряженную с плоскостью предмета, то коэффициенты а, а. и должны быть равны нулю. Определим более точно вид разложения {I, т, М) и /2 (/, т, М). С этой целью установим существование функции S, частные производные от которой по ее аргументам как раз равны и /2; эта функция S играет роль потенциала аберраций. Симметрия системы позволяет легко представить разложение функ ции S в ряд по степеням ее аргументов и по этому разложению решить поставленный вопрос. Уравнение поверхности волны Рассмотрим поверхность волны пучка лучей, исходящих из светящейся точки А, лежащей в меридиональной плоскости.* После выхода из оптической системы 00 эта волна, претерпев-•1 шая на каждой преломляющей по- верхности изменение формы, больше не является сферической. Ее отступление от сферической формы может быть определено отрезком N, представляющим собой отсчитываемое по нормали расстояние между реальной волной и идеальной волновой поверхг ностью, определяемой центром в точке Ло (идеальном изображении точки Л1) и радиусом R, равным расстоянию между плоскостью изображения и плоскостью выходного зрачка. Пусть ОХ (рис. И.5) - оптическая ось системы; О - начало координат; XOY - меридиональная плоскость, содержащая гауссово изображение С светящейся точки, причем С находится на расстоянии /о от оси. Пусть S - идеальная волновая поверхность с вершиной в точке О и радиусом ОС R; М - некоторая точка этой поверхности; МК - нормаль к волновой поверхности в этой точке; К - точка пересечения нормали с реальной волновой поверхностью. Уравнение идеальной волновой поверхности имеет вид (x~df+{y-i;f + z-R" = 0, где d - абсцисса точки пересечения плоскости установки с осью ОХ. 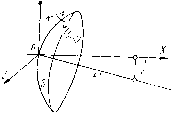 Рис. II.5 Можно написать уравнение реальной волновой поверхности в таком виде: /(х, у, Z) = {x-df + {У~ Iof + z- (R + N) = О, где N - отрезок МК - некоторая функция от г/ и от г. Уравнение нормали к реальной волне в точке с координатами у, г и X имеет вид Х~х Y -у 7. - Z 3 дг дх ду откуда, пренебрегая величиной N по сравнению с R и помня, что N - функция от у и г, получаем Х-х Y-y x - d (II.9) dy " " dz Полагая в последнем уравнении X = d, получаем значения координат Z = 60, У k + 6g точки пересечения луча с плоскостью установки, а именно: 6G = R 6g = R dN dy (11.10) Уравнения (11.10) связывают поперечные аберрации 6G и 6g с производными от функции N по г я по у. Остается теперь выразить последние координаты через известные т и М. Если аберрации системы невелики, то можно принять, что направление реального луча, проходящего через точку М идеальной волновой поверхности с координатами х, у, г, мало отличается от направления нормали МС, т. е. можно принять, что реальный луч проходит через точку С с координатами d, lo и О. Положим, что плоскость уОг совпадает с плоскостью выходного зрачка и что координаты точки пересечения луча с этой плоскостью суть О, т и М. Так как эти координаты должны удовлетворять уравнению прямой, проходящей через точки УИ и С, то они связаны следующими соотношениями: d - x z; т = dy - xIq i - x (11.11) d-YR-z-iy-kf- Эти приближенные . уравнения дают достаточную точность для всех случаев, встречающихся на практике, так как нормали в соответственных точках обеих волновых поверхностей - реальной и идеальной сферической - мало отличаются друг от друга. Если угол расхождения выходящего пучка невелик и отношение диаметра выходного зрачка к расстоянию d (или R) не превышает 1 :4 и даже I -.3, то формулы (11.11) могут быть упрощены следующим образом. Положим, что d = тогда обычным приемом разложения корня квадратного в ряд по формуле бинома Ньютона находим Далее, используя формулы (II.И) и помня, что х мало по сравнению с d, получаем приближенные формулы для /« и М в таком виде: "аГдим"""" " ™ "---ш приближенным значением У = m (П.12) Наоборот, у и z выражаются через М и т следующим образом: г = М 1- (11.13) 6G = r: dN дМ (11.14) Волновая аберрация N представляет собой функцию от у и г, т. е. от координат точки пересечения луча со сферой S. Но координаты у и z могут быть выражены через т и М, поэтому функция N может быть разложена в ряд по степеням т и М. Она зависит также от конструктивных элементов системы и от положения плоскости предмета, но в данном вопросе эта зависимость может 58 tie приниматься во внимание. Сопоставляя уравнения (II.8) и (11.14) и помня, что коэффициенты а- = а. = аз = О и что т = = рт и УИ = с точностью до членов третьего порядка малости, мы видим, что разложение функции N начинается с членов четвертого порядка малости. Рассмотрим теперь, как использовать симметрию системы для определения числа коэффициентов разложения. Каноническая форма уравнения поверхности волны В выражение всякой функции от нескольких переменных входит еще ряд коэффициентов, число которых путем специального выбора системы координат или введением новой системы переменных может быть, доведено до минимума. Например, уравнение конического сечения в прямоугольной системе координат имеет вид Ах + Вху+Cy + Dx + Ey + F = 0 с шестью коэффициентами А, В, С, D, Е, F. Но особым выбором осей координат это уравнение может быть приведено к виду г 62 - где имеется только два коэффициента а и Ь. Никакими способами коническое сечение не может быть представлено меньшим числом параметров. Волновая аберрация N представляет собой функцию четырех параметров, например у, z, т, М {за у я z здесь принимаем координаты точки пересечения луча с плоскостью предмета). Если разложить эту функцию в ряд по степеням величин у, г, т и М, то в общем случае будет 1 член нулевого порядка, 4 члена первого порядка, 10 (1 -Ь 3 + 6) членов второго порядка, 20 (1 + 3 + 6 + 10) членов третьего порядка и 35 (1 + 3 + 6 + 4- 10 + 15) членов четвертого порядка (столько членов, сколько имеется частных производных того же порядка). Особым выбором системы координат (перемещением начала координат и изменением направления осей) число членов может быть уменьшено на не-•сколько единиц. Насколько деликатен вопрос о минимальном числе независимых коэффициентов функции, можно иллнхтрировать двумя примерами из теории аберраций. Пецваль, первым давший разложение в ряд аберраций пятого порядка, насчи-тал 12 коэффициентов; Шварцшильд нашел всего 9. По поводу этого числа возникла полемика между Кербером и Зоннефельдом; Кербер, проделав разложение гДругим методом, подтвердил результаты Пецваля, в то время как Зоннефельд доказал правильность вывода Шварцшильда. Победа осталась за последним. : Лармор насчитал 7 независимых коэффициентов в разложении эйконала Второго порядка общей оптической системы; Смит и после него Герцбергер показали, что это число может быть сведено к 6 (вместо 10 при случайном выборе ко-;ординатной системы), Если оптическая система обладает осью симметрии, то функция N по-прежнему зависит от четырех переменных: у, г, т и М, но эти четыре переменные могут входить в выражение для Л только в определенных комбинациях, обусловливаемых осевой симметрией. Пусть ОХ (рис. П.6) - оптическая ось системы; А {у, z) - точка, где луч пересекает плоскость предмета; Р (т, М) - точка, где луч пересекает плоскость выходного зрачка; Ф и Tjp - углы, образуемые с меридиональной плоскостью радиусами-векторами OA = г и ОР = г. Положение луча АР по отношению к оси симметрии ОХ определяется тремя параметрами, например расстояниями OA и ОР" разностью углов ф - -ф; все эти три величины при вращении луча АР относительно оси остаются постоянными. Но 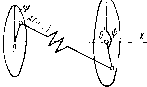 p(in,nj Рис. 11.6 г/ = гсо5ф; т= rcosTJ;; г = /-51пф; Л4= гsin г5. Следовательно, постоянными остаются величины R=y + z = r Rp = m+ М= г; и = ут + zM = гг cos (ф - г);). Так как положение примой АР относительно оси OA полностью определено тремя величинами R, R и (ф-ф), то N может зависеть от у, г, т и М только через их функции R, Rp и и. Так как это функции второго порядка относительно у, z, т и М, то величина yV), т. е. сумма всех членов N, порядок которых равен четырем, может быть составлена только из шести комбинаций, а именно R", rI, u, RRp, Ru, RpU, и имеет вид Л* = + 4 + + 4 + + где А, В, . . ., F - некоторые постоянные, зависящие только от конструктивных элементов системы; численные коэффициенты и поставлены для удобства дальнейших выкладок. С целью упрощения выберем плоскость XOY так, чтобы она проходила через точку объекта; тогда г = 0. Дифференцируя последнее уравнение, вычисляя производные согласно (П. 14) и заменяя величины R, Rp и и их выражениями, получаем 8g = R [Вт (т2 + М) + F (Зт + М") у + + {2С + 0)ту + ЕуП; 8G ==R [ВМ (т2 + м2) + 2mMyF + DMy\ Члена, содержащего коэффициент А, нет, и остались только Шены, зависящие от В, С, D, Е, F. Каждый из этих членов соот-ртствует некоторой комбинации произведений величин г/, т, и, причем сумма степеней всегда равна трем. Отсюда и произошло Название «аберрации третьего порядка», данное этим членам. оложим RB = Л1, RF = Б1, (2С + D) R = С„ RЕ = Е, I Для bg и бС получаются следующие формулы: у = Ат(т2 + /W3) + BJ{3m"" + М) + CJbn + ЕР; f 6G =/li/M(m2 + Af2)-2fii nM + £>i/2Af, / (f-) рде Ax, Bl, . . ., £1 - коэфициенты, зависящие только от по-ргоянных оптической системы и от положения плоскостей объекта й в.ходного зрачка, но не зависящие от координат луча; послед-рй определяется четырьмя координатами: двумя в плоскости Объекта (у = /, г = 0) и двумя координатами пересечения луча I плоскостью выходного зрачка (т и М). Впрочем, можно за-аенить координаты в плоскости выходного зрачка т и М коорди-яатами точки пересечения луча с плоскостью входного зрачка т а М. Для этой цели пользуются соотношениями т = тр, Ц - Мр, верными только в гауссовой области; но при рас-отрении аберраций третьего порядка такая замена не меняет результатов, и мы получаем формулу точно такого же вида, как вормула (11.15), где коэффициенты А, . . ., Ei имеют иное чис-иенное значение. Изображение точек при наличии аберраций й Как уже было указано, гомоцентрический пучок лучей, вышед- 1ИХ из какой-нибудь точки пространства предметов, после про-)ждения через оптическую систему вследствие наличия аберра-1Й оказывается не гомоцентрическим; лучи его не пересекаются одной точке и поэтому в плоскости гауссово го изображения )разуют размытое светлое пятно - пятно рассеяния. Фор-лы (11.15) дают возможность определить точку пересечения ллоскостью изображения каждого отдельного луча из числа разующих пучок, если оптическая система обладает аберра-ями только третьего порядка. Чтобы исследовать распределеиие точек пересечения с пло-)стью изображения отдельных лучей данного пучка, обычно --тьзуются следующим приемом: из всего пучка рассматривают Ш1рерывную совокупность лучей, выходящих из одной точки юйдмета и по выходе из системы пересекающих плоскость выход-го зрачка по окружностям с центром на оси системы. Каждая такая совокупность лучей в плоскости изображений 1ет систему точек пересечения, геометрическое место которых (0) (1) (2) (3) (4) (5) (6) (7) (8) ( 9 ) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) (51) (52) (53) (54) (55) (56) (57) (58) (59) (60) (61) (62) (63) (64) (65) (66) (67) (68) |
|
|