vou в его начало и 0,25 = Р9, имел внд: f Fsin - ИПЭ -. Вы-числения велись прн = i-lO-".

Гарантированную сходимость при простой программной реализации имеет метод деления отрезка пополам. В нем интервал [а, Ь] делится пополам, затем выбирается тот полуинтервал, в котором F{x) переходит через нуль, он делится вновь пополам н т. д., пока ширина суженного интервала не станет меньше в [4, 5].

Программа 5.22. Реализация метода деления отрезка пополам. Ввод: данные F (х) при д:->-РА, а = РА, (& -а)= РВ, любое число со знаком, совпадающим со знаком F{a), п = PC и г = РД.

ИПВ 2-4- ПВ t ИПА + ПА Fx

ИПД - Рл: < О 16 ИПА С/П ............

ИПС XY ПС X Рл: < О 00 ИПВ /-/ БП 01

Решим для контроля этой программы уравнение f (t/д) = £ - С/д -/?/о (ед - О = О,

определяющее падение напряжения на диоде х = С/д, подключенным через резистор R к источнику напряжения Е. Тогда при £=Р1, i?/o = P2 н v = P3 фрагмент программы, вычисляющий f (л:) =f (t/д), имеет вид

ИПА ИПЗ X Fe* 1 - ИП2 X ИПА + ИШ XY -

Для £ = 0,5 В; /а/г=МО- В; v = 20 1/В; n = f(0)=0,5, а = О, Ь==0,5 В н 6=1-10- получим С/д = 0,27172852 при и ял 2 мин и при г = ЫО-* t/д = 0,27174234 В при ?с « 4 мин. Из этого примера видно, что сходимость метода деления отрезка пополам медленная, ибо функция F(x} = F(U) относительно простая.

Гарантированную сходимость имеет также метод случайных проб (Монте-Карло). В нем приближениям Ха, Ху, Хг, Хп задают случайные значения в интервале [а, Ь], каждый раз сужая этот интервал. Например, если значения f(a)>0 и (л:„)>0 функции F{x), то а присваивается значение Хп, если F(x„)< О, то b присваивается значение х„ и т. д. до тех пор, пока разность b - а не станет меньше е. Генерация случайных чисел с равномерным распределением описана далее в § 5.12.

Программа 5.23. Реализация метода случайных проб. Ввод: данные F{x, при х„ = РС, начальное случайное число К» == РО (Vo < 1), о = РА, 6 = РВ, е = РД.

ИПО 3 7 X 1 -f- ПС кипе XY ИПС - ПО ИПВ ИПА - X ИПА + ПС

......... Рл:>0 N ИПС ПА БП (/V+2) ИПС

ПВ ИПВ ИПА - ИПД - Fx < О 00 ИПА С/П

• в этой программе Л/- число, даюшее номер шага команды ИП., после записи в программу фрагмента, вычисляющего F{x„). Для иредшествующего примера при Vo = 0,1234567, g = 0,5 В = PI, /о/ = 1 • 10-S В = Р2, V = 20 1/В = РЗ, а = 0,2 В = РА, Ь = = 0i3 В = РВ и 8 = МО- = РД получим = 0,27144498 В при I =*70 с. Фрагмент программы вычисления F{x„) имеет при этом гид;

ИПЗ X Fe* I - ИП2 X ИПС + ИП1 XY -

Процесс формирования значений л;», xt, Xi, дг„ можно упорядочить, в частности, формируя эти значения поразрядно [8]. Например, можно формировать значения Хп с шагом

вычисляя каждый раз F(x„). Если f (дгя)/Лзд О, даем Хп очередное приращение &Хц. Если F{xn)/AxN < О, то делям Ахн на некоторое число -R (показатель разрядности), т.е. получаем новое значение

Если (Ахц) > е, вычисляем х„ по формуле (5.17), если {Ахк)е, заканчиваем счет. При Л = Ю метод поразрядного приближения становится методом подекадного приближения [8], причем результат вычислений автоматически усекается (точными являются все цифры результата).

Программа 5.24. Реализация метода подекадного приближения. . Ввод: данные F{x„) при х„ -* РА, Хе = РА, Axi = РВ и е = PC

ИПА ИПВ 4- ПА ..................

......... ИПВ -t- Fx < О 00 ИПВ /-/ I

О -г- ПВ Fx ИПС - Fx < О 00 ИПА СГ

Для приведенного выше примера при ДУд,=Дх1=0,1 В и е2:=Ы0-« получим £/д=0,272 В при tc»65 с.

Ввиду невысокого быстродействия микро-ЭВМ индивидуального пользования значительный интерес представляют методы решения нелинейных уравнений, обеспечивающие повышенную скорость сходимости итерационных процессов. ;

Корень уравнения (5.12) можно найти путем обратной интер* поляции/экстраполяции. При этом в интервале [а, Ь] задается Л зна« чений абсцисс х„ и вычисляется Л ординат f (х„). Записав вначе-нйя х„ в регистры, отведенные в программах интерполяции с произ- вольно расположенными узлами (§ 5.2) под запись ординат, в зна чеиия f (Хп) -в регистры, отведенные под запись абсцисс, найдем" сразу приближенное значение корня Хи После SToro можно сузить интервал [а, Ь] и повторить расчет.

программа 5.25. Реализация метода нахождения корней с по. мощью квадратичной обратной интерполяции/экстраполяции. Ввод: данные F(х) при заносимом в начало подпрограммы, хо = РЛ, ;«1 = РВ и Ха = PG.

ИПА ПП 46 ПО ИПВ ПП 46 П1 ИПС ПП 46 га ИПВ ИПА - ИП1 ИПО - -i- ПВ ИПС ИПА - ИП2 ИПО - ИПВ - ИШ

ИП1 - ПС ИП1 /-/ ипа X ипв +

ИПО /-/ X ИПА + С/П ......... В;0

Пусть надо найти напряжение на стоке мощного МДП-транзи-Стора (рис. 5.2, о и б) из решения уравнения

(5.18)

если зависимость тока стока от напряжений на стоке и затворе (/3 описывается выражением

1 е-Рс/(Уз-£о-*1)

, (5.19)

где S -крутизна, р и Ь - параметры аппроксимации вольт-амперноц характеристики.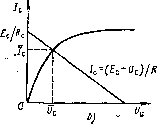

(>.

а; ,

Ряс. 5.2. Каскад на мощном МДП-транзисторе (а) и графическое определение положения его рабочей точки (б)

Подставляя (5.18) в (5.19), получим окончательно

F (UJ =.Е,-и- R,S {bUl -U, + t/o)

(5.20)

При Яд = P4, = P5, SR = P6, p = P7, Ь = P8 и Uo= +1 В •пясыраемый в подпрограмму фрагмент вычисления функции F(U) имеет вид:

t ИП7 X ИП8 ИП5 Fx X 1 + ИП5 - П9 ч- Fe* 1 - ИП9 Х ИПб Х

+ ИП4 XY -